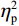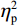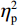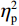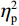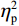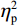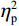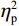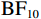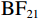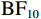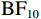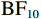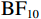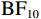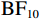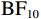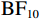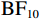高水平运动员的动作预判能力优势已经在大量研究中得到验证，他们能够通过观察对手或同伴的身体运动学信息提前准确预测动作结果^[1]。在体育比赛中，尽管动作预判的优势为运动员的动作响应提供了先行保障，但对预测结果的有效监控同样是高水平运动表现不可或缺的一环。研究^[2−3]发现，专项运动经验可以提高个体对运动序列中错误信息的敏感性，使运动员能够及时调整以应对意外情况。然而，目前尚不清楚在动作预测的基础上，专项运动经验如何影响动作监控的认知过程，特别是在处理观察到的结果与预测结果之间偏差的响应过程方面。

从动作预判到动作执行，有效地感知和识别预期偏差是决定动作输出质量的关键。以乒乓球运动为例，运动员借助球拍与球接触前的运动学信息，能够提前预测球的飞行方向^[4]，并在发现球的实际飞行轨迹与预测存在差异时迅速进行动作计划（motor planning）的调整，以此来使错误预期或误导性动作可能带来的负面影响最小化。当实际结果与预期存在明显差异时，会引发针对认知冲突的解决机制。反之，如果实际结果与预期的偏差在可控范围内，只需通过在动作控制（motor control）阶段进行微小的调整即可减轻偏差效应。电生理学研究^[5]也支持这一认知过程的存在，发现在完成动作预期后，额-中央区的Theta振荡开始激活，并在实际动作结果与预期不一致时显著增强，而在两者相符时减弱。因此，感知和识别预期偏差对于运动员应对潜在赛场冲突至关重要，是保障其完成流畅互动的重要环节。

根据视觉的知觉-动作双系统理论（perception-action double-system theory），当执行目标导向动作时，视觉系统被划分为背侧通路和腹侧通路2个独立的子系统^[6−7]。背侧通路主要负责外部信息的表征，腹侧通路则负责动作指导。这2个子系统通过并行的认知过程协同工作，共同支持动作的准确执行^[8]。这一理论在一定程度上有助于解释基于动作预期的偏差监控过程。在复杂的体育运动中，动作预期引发的目标导向动作需要视觉系统处理目标信息，并与预期目标进行对比，调整动作计划或控制参数，以实现目标导向动作的精确执行。Spinelli等^[9]的研究表明，个体在表征不同程度的偏差或冲突时采用了分级化的方式，而非全或无的规则，并且这一发现在与偏差相关的脑电成分的潜伏期和振幅上得到了验证。这种分级化的策略有助于个体对他人动作进行更有效的监控，从而促进实现人际互动式的目标导向动作。基于动作预期的目标导向动作涉及对预测偏差的视觉感知加工和依据偏差大小进行的动作调整2个过程。具体而言，个体首先通过运动学信息对动作结果进行预判，并生成相应的动作计划；随后，通过视觉捕获实际动作结果，并与预期结果进行比较，识别预期偏差。在此阶段，负责知觉任务的腹侧通路存在感知偏差，负责动作任务的背侧通路则依据偏差大小进行动作计划的更新或修改。在这一过程中，后者属于更加主观的策略性加工，前者则更依赖于原有的动作预判能力。尽管双系统理论为理解基于动作预判的偏差监控提供了框架，但目前还没有直接的研究证据量化这2个过程的具体作用。

动作预判中的偏差感知主要取决于个体动作预判的准确性。根据贝叶斯模型，更加精准的内部模型能够减少预测结果的不确定性，从而提高动作预判的准确性^[10]。长期的运动经验有助于运动员构建更为完善的内部模型，这不仅提高了预判的准确性^[11−12]，还增强了对偏差的敏锐感知^[13−14]。明显的预期与实际结果偏差能够帮助运动员快速更换原有动作计划，以应对偏差诱发的冲突决策。贝叶斯模型表明，预期偏差的大小并非绝对的二元分布，而是遵循正态分布。这意味着在处理高不确定性的预期偏差时，个体需要更为精细的决策来调整目标导向动作。长期运动经验使运动员形成了应对不确定性的特定认知策略，如乒乓球运动员会将更多视觉资源保留在低确定性目标中，而将运动资源投入于高确定性目标，以保证在对高确定性结果进行快速响应的同时，降低意外结果所造成的损耗^[15−16]。由此，推测，在预期偏差监控过程中，存在对不确定性较高的预期偏差做出细微调整的需求。这一过程符合双系统理论中腹侧通路的处理方式，实现在指导动作维度上的偏差决策。因此假设，运动经验对动作预期偏差监控过程的影响是复杂而多层次的：首先体现在偏差感知中，只有具备有效内部模型的个体才能准确感知偏差；随后当偏差大小无法快速表征为一致或冲突时，就需要对这种不确定性进行决策。尽管运动经验不会影响这一加工过程的发生，但个体长期形成的策略会导致具体的加工方式呈现经验性差异。

为深入探究上述假设，以乒乓球发球动作为背景（该动作具有清晰可辨认的动作预判和预判结果监控过程），通过一系列发球动作与动作结果存在不同程度偏差的刺激材料，要求被试判断基于发球动作形成的预期结果是否与观察到的动作结果存在偏差，并据此做出相应决策。同时，采用漂移扩散模型（Drift-Diffusion Modeling，DDM）对决策的选择和反应时间的分布进行分析。DDM将决策过程描述为对决策相关证据不断积累的过程，一旦支持特定选择的累积证据量达到阈值或边界，可以用以模拟乒乓球运动员根据感知和运动信息做出是否存在预期偏差决策的认知过程 ^[17−19]。DDM的核心参数包括起始点（starting point，z）、漂移率（drift rate，v）、决策阈值（decision threshold，a）和非决策时间（non-decision time，t），其中：z代表决策过程开始时对决策项的初始偏好或倾向性，在本文中代表在观察完整发球动作和结果后，被试基于内部模型形成的对预期结果和实际结果之间偏差的感知，用以量化决策过程中的感知维度加工；v代表证据积累的速度和方向，本文模拟了被试根据目标动作的调整策略来决策是否存在偏差，以此量化决策过程中的动作维度加工；a是指在决策过程中设定的2个阈值，用于判断何时做出决策；t是指除了决策过程之外用于感知、理解和做出反应的时间，如加工信息和做出按键反应的时间^[18]。利用DDM中的z参数和v参数将潜在的认知过程分解成模型的不同组成部分^[20]，实现对感知与动作决策过程的定量分离。

根据双通路模型和先前的研究，预期新手的决策模型主要由漂移率决定，而运动员的决策模型受到起始点和漂移率的共同影响，并且起始点的影响可能在具有明显偏差的情况下更为显著。这一差异反映了2组被试在加工策略上的根本区别，为理解运动经验如何影响偏差感知与动作调整提供了新视角。

1.   研究对象与方法

1.1   研究对象

按乒乓球运动经验在上海市招募运动员组和对照组被试共76名。运动员组43人（20男，23女），平均年龄为19.97周岁，平均训练年限为10.09年。对照组33人（16男，17女），平均年龄为20.07周岁。乒乓球运动员组被试需要满足：①运动等级均达到国家二级及以上水平；②专业训练年限为8年及以上；③近3年每周训练超过20 h。对照组被试需要满足：①无乒乓球及其他持拍球类运动经验；②较少或不关注乒乓球比赛。所有被试均为右利手，视力或矫正视力正常，健康状况良好，无精神疾病史。被试在实验前知晓并签署知情同意书。使用G*Power软件进行敏感性分析，结果显示，在0.95的功效水平（β）、0.05的显著性水平（α）以及重复测量之间的相关性（r）为0.5的情况下，进行2×7重复测量方差分析检测到的效应值（f）大于0.14。本实验已通过上海体育大学伦理委员会批准（102772020RT111）。

1.2   研究方法

1.2.1   实验设计

采用2（运动经验：运动员组、对照组）×7（运动学信息与飞行信息的不一致程度：根据发球动作真实落点与视频呈现落点之间的偏差程度分为7等份）被试间设计，其中，运动经验为组间变量，运动学信息与飞行信息之间的不一致程度为组内变量。

1.2.2   刺激材料

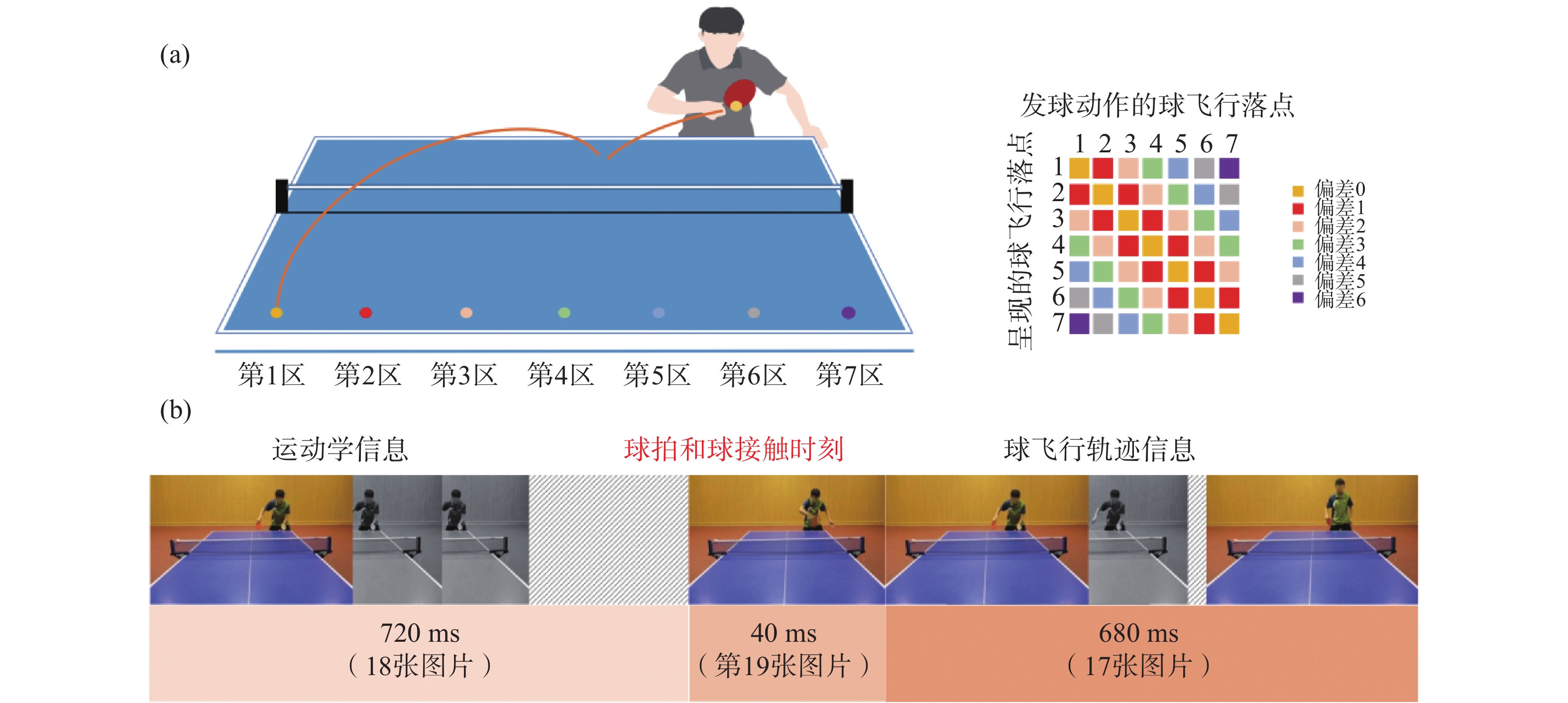
刺激材料为自行录制和编辑的反手发球动作。发球手为一名右手持直拍的在役乒乓球运动员（男，20岁）。发球手站于球台左侧进行反手下旋发球，发球落点为接发球方从左往右平均分后的7个区域。录像设备为Canon 5D Mark Ⅲ，分辨率为(1280×720) px。

刺激材料由Adobe Premiere软件（Adobe Systems Incorporated，San Jose，CA，USA）进行处理。首先选择21段拍摄质量清晰的发球视频，分辨率统一为(640×360) px，25帧/s；每个落点区域取3段，并对面部信息进行模糊处理。随后将发球动作与球的飞行轨迹进行重新组合，构成7种不同偏差程度的刺激材料（偏差0～6）。偏差程度是指发球动作的球飞行落点与重新组合后呈现的飞行落点之间的不一致程度（表1）。刺激材料在重新组合后，以球与球拍接触为零点，向前18帧为起始发球动作，向后17帧为触球后的球飞行轨迹信息，共36帧刺激视频。

表  1  刺激材料的变量设置及对应的具体落点

Table  1.  The variable settings of stimulus materials and their corresponding landing zones

偏差程度	发球动作的落点区域（剪辑呈现的落点区域）
偏差0 （无偏差）	1（1）；2（2）；3（3）；4（4）；5（5）；6（6）；7（7）
偏差1	1（2）；2（3）；3（4）；4（5）； 5（6）；6（7）；2（1）；3（2）；4（3）；5（4）； 6（5）；7（6）
偏差2	1（3）；2（4）；3（5）；4（6）；5（7）；3（1）；4（2）；5（3）；6（4）；7（5）
偏差3	1（4）；2（5）；3（6）；4（7）；4（1）；5（2）；6（3）； 7（4）
偏差4	1（5）；2（6）；3（7）；5（1）；6（2）；7（3）
偏差5	1（6）；2（7）；6（1）；7（2）
偏差6	1（7）；7（1）
注：以球落在第1区的发球视频为例，将其运动学信息图片和原始球飞行轨迹信息图片（即落点在第1区）的组合设定为偏差程度为0的刺激材料，依此类推，将其运动学信息图片和落点在第7区球飞行轨迹信息图片的组合设定为偏差程度为6的刺激材料 （图1）。偏差程度数值越大表示实际球飞行轨迹与观察到的球飞行轨迹之间的偏差越大。

下载: 导出CSV 

| 显示表格

图  1  偏差决策刺激材料的分区与呈现

注：图（a）为实际球飞行轨迹与观察到的球飞行轨迹之间的偏差程度，7种颜色代表7种偏差刺激材料；图（b）为连续图片示例，每个刺激材料包含球拍和球接触前的18帧、球拍和球接触时的1帧以及球拍和球接触后的17帧。

Figure  1.  Partitioning and presentation of deviation decision stimulus materials

下载: 全尺寸图片 幻灯片

1.2.3   实验任务与流程

实验在隔声、隔光且安静的房间进行，被试与电脑显示器之间的距离约为 60 cm，显示器为17英寸，分辨率为(1024×768) px。被试在实验过程中注视屏幕中央，并将左手和右手的食指放在键盘的F键和J键上。指导语中告知被试呈现的发球动作和动作结果（即球的飞行方向）可能非真实落点，要求其在视频结束后按键判断呈现的飞行落点与其预判的落点是否一致。在每个试次中，首先呈现1000 ms的注视点，随后呈现1440 ms的发球视频，刺激呈现后，要求被试在“请回答”界面快速按键，F键为一致，J键为不一致。

正式实验共4组，每组包含40个试次，每组内试次的偏差程度条件随机呈现，并且组块间的偏差程度条件顺序均不同。在正式实验前，提供14个练习试次以熟悉实验任务。本实验的行为数据通过E-prime 3.2软件采集。

1.2.4   数据分析

（1）行为数据处理。计算被试在7种偏差条件下的判定偏差比例（判断为“不一致”的比例）和平均反应时。对平均反应时进行预处理，剔除反应时超过3000 ms或少于100 ms的异常试次^[2]，剔除率为1.7%。

基于信号检测论^{[5, 14, 21]}，计算辨别力指数d'作为评价偏差感知敏感性的指标。以在无偏差条件（即偏差0）下判断“无偏差”为正确拒绝、“有偏差”为虚报，以在有偏差（即偏差1～6）条件下判断“有偏差”为击中、“无偏差”为漏报，分别得到偏差1～6条件下的偏差敏感性指标。

对判定偏差比例和反应时分别进行2（组别：运动员组 vs. 对照组）×7（偏差程度：0～6）的重复测量方差分析，对d'进行2（组别：运动员组 vs. 对照组）×6（偏差程度：1～6）的重复测量方差分析，组别为组间变量。数据采用SPSS 20.0软件进行分析，对不满足球形检验的统计量采用Greenhouse-Geisser法矫正自由度与P值，事后检验采用Bonferroni方法，以P<0.05为结果显著。

（2）漂移扩散模型。通过使用Python工具箱的HDDM^[22]对各偏差条件反应时和偏差决策（判定为一致或不一致）数据进行DDM建模。HDDM使用分层贝叶斯参数估计（hierarchical Bayesian parameter estimation）的方法拟合每个被试数据的同时估计每个个体（individual）与群体（group）层面的DDM模型参数，并允许以联合后验分布（joint posterior distribution）的方式量化所有模型参数的估计不确定性^[22]。由于HDDM对异常值敏感，除上述排除异常值的步骤外，还采用HDDM中包含的异常值混合模型，并将异常值的概率设置为0.05^[22−24]，进一步排除异常值。

在确立DDM模型参数时，首先建立一系列在认知层面上合理的不同模型，通过模型比较，确定最能解释数据的模型。所有模型都对每个被试的3个与决策相关的参数（v、a和z）和1个与非决策相关的参数（t）进行估计。这些模型分别对运动员组数据和对照组数据进行估计，因此每个被试的模型参数是唯一的，但是这些参数是从相应群体水平的分布中抽取的^{[22, 25]}。接下来采用HDDM回归模型检验v、a和z各决策相关参数与偏差程度条件之间的关系。基线模型假设所有参数都可以自由变化；随后创建3个模型，其中，1个模型的决策相关参数随偏差程度的变化而变化，另2个模型的参数自由变化；然后，另外创建3个模型，其中，2个模型的决策相关参数随偏差程度的变化而变化，另1个模型的参数自由变化；最后，又创建1个模型，允许所有决策相关参数都随偏差程度的变化而变化。总共生成了8个不同的模型。

采用层次贝叶斯马尔可夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）抽样方法来估计4个参数（a、v、z和t）的后验分布^[26]。每个模型共抽取了5000个样本，前1000个样本被丢弃（burn-in）。为确保MCMC链的收敛性，检查每个估计参数的后验跟踪（posterior traces）和自相关图（autocorrelation plots），并为每个参数计算Gelman-Rubin统计量（R hat值）^[27]。通过比较模型之间的偏差信息准则（Deviance Information Criterion，DIC）确定最佳拟合模型（表2）。

表  2  各竞争模型的偏差信息准则（DIC）

Table  2.  The deviance information criterion (DIC) value for each of the competing models

模型	模型参数	运动员组DIC	对照组DIC
模型1	none	9899.26	9599.44
模型2	z～contrast	9636.22	9553.92
模型3	v～contrast	9303.57	9449.14
模型4	a～contrast	9917.42	9603.52
模型5	z～contrast, v～contrast	9296.60	9459.34
模型6	v～contrast, a～contrast	9311.44	9450.28
模型7	z～contrast, a～contrast	9633.26	9560.47
模型8	z～contrast, v～contrast, a～contrast	9308.82	9465.69

下载: 导出CSV 

| 显示表格

2.   研究结果

2.1   判定偏差比例和反应时结果

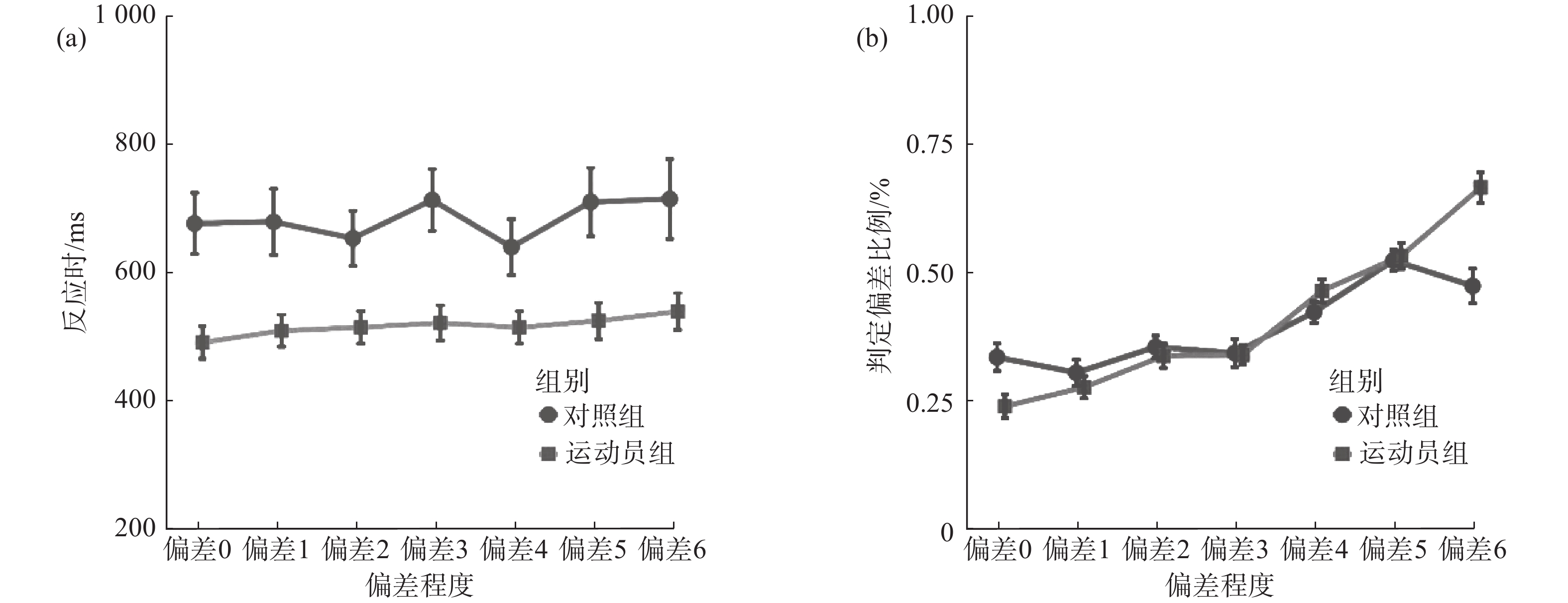
判定偏差比例的方差分析结果显示，偏差程度主效应显著（F_{(3.15, 233.12)} = 66.31, P < 0.001, $ {\eta }_{\mathrm{p}}^{2} $ = 0.47），组别与偏差程度交互作用效应显著（F_{(3.15, 233.12)} = 10.10, P < 0 .001, $ {\eta }_{\mathrm{p}}^{2} $= 0.12）。事后比较发现，对于运动员组，除偏差0和偏差1以及偏差2和偏差3之间无显著差异（Ps > 0.45），其他偏差程度条件间的判定偏差比例均存在显著差异（Ps < 0.043）。相比之下，对照组在偏差0～3条件之间、偏差4和偏差6之间以及偏差5和偏差6之间均未发现显著差异（Ps > 0.20）。这表明相对于对照组，运动员组能更好地、更细微地识别实际球飞行轨迹与观察到的球飞行轨迹之间的偏差[图2（a）]。组别主效应不显著（F_{(1, 74)} = 0.34, P = 0.056, $ {\eta }_{\mathrm{p}}^{2} $= 0.01）。反应时的方差分析结果显示，偏差程度主效应显著（F_{(4.74, 350.60)} = 3.01, P = 0.013, $ {\eta }_{\mathrm{p}}^{2} $ = 0.04），表明反应速度总体上随偏差程度的变化而变化。具体而言，被试在偏差0（584.39 ms）、偏差1（594.76 ms）、偏差2（584.56 ms）和偏差4（577.60 ms）条件下反应时相对较短，而在偏差3（617.90 ms）、偏差5（617.97 ms）和偏差6（627.53 ms）条件下反应时相对较长。组别主效应显著（F_{(1, 74)} = 11.68, P = 0.001, $ {\eta }_{\mathrm{p}}^{2} $ = 0.14），表明运动员组的反应时（M = 517 ms）比对照组（M = 684 ms）更快[图2（b）]。组别与偏差程度交互作用效应不显著（F_{(4.74, 350.60)} = 1.22, P = 0.30, $ {\eta }_{\mathrm{p}}^{2} $= 0.02）。

图  2  运动员组和对照组在各偏差程度条件下的反应时（a）和判定偏差比例（b）

Figure  2.  Reaction time (a) and proportion of classified discrepancy (b) across discrepancy conditions and groups

下载: 全尺寸图片 幻灯片

2.2   信号检测论分析结果

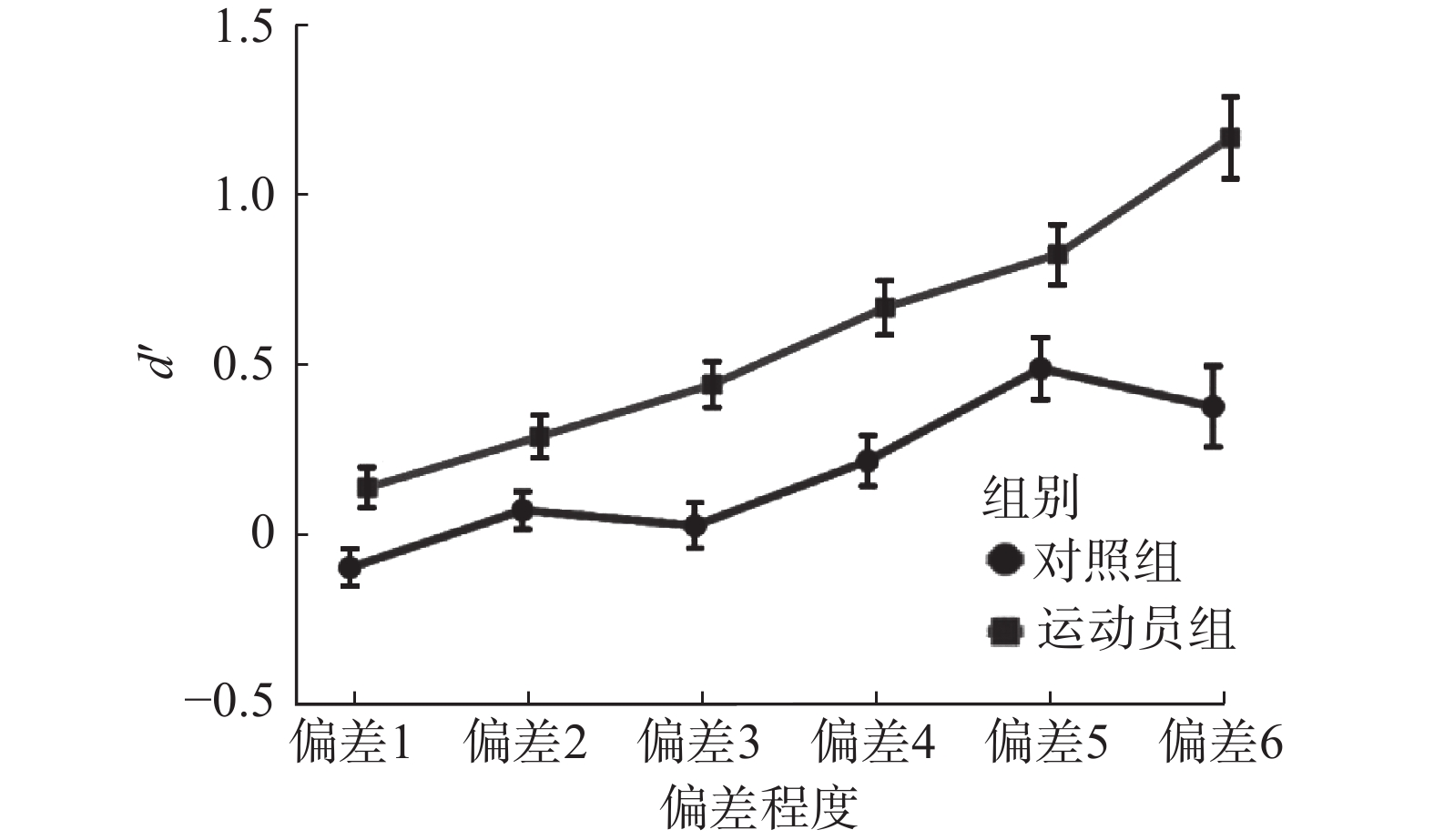
d'的方差分析结果显示，偏差程度主效应显著（F_{(3.65, 270.24)} = 31.41, P < 0.001, $ {\eta }_{\mathrm{p}}^{2} $ = 0.30），表明偏差程度越大，被试越能够识别实际球飞行轨迹与观察到的球飞行轨迹之间的偏差。组别主效应显著（F_{(1, 74)} = 17.17, P < 0.001, $ {\eta }_{\mathrm{p}}^{2} $= 0.19），表明运动员组（d' = 0.59）比对照组（d' =0 .20）在识别偏差方面更有优势。此外，组别与偏差程度交互作用效应显著（F_{(3.65, 270.24)} = 4.62, P < 0.001, $ {\eta }_{\mathrm{p}}^{2} $ = 0.06）, 表明随着差异度的增加，群组之间识别偏差能力的差异也随之增加。事后比较发现，在所有偏差程度条件下，运动员组的d'均高于对照组（Ps <0 .044，图3）。

图  3  运动员组和对照组在各偏差程度条件下的d'

Figure  3.  d' of the expert group and the control group

下载: 全尺寸图片 幻灯片

2.3   漂移扩散模型结果

对于运动员组，最优模型（即DIC分数最低的模型）是漂移率和起始点随偏差程度变化而变化，同时允许决策阈值自由变化的模型（表2中的模型5）。对于对照组，最优模型是漂移率随偏差程度变化而变化，同时允许决策阈值和起始点自由变化的模型（表2中的模型3）。运动员组和对照组的所有模型参数在五次重复链上的Gelman-Rubin统计量均低于1.1。后验跟踪和自相关图也确认了每个参数的充分收敛性。因此，在JASP 0.17.1.0中使用默认的先验值（jasp-stats.org；JASP团队，2016年）进行进一步分析，关注最优模型的模型参数估计值。

2.3.1   漂移率

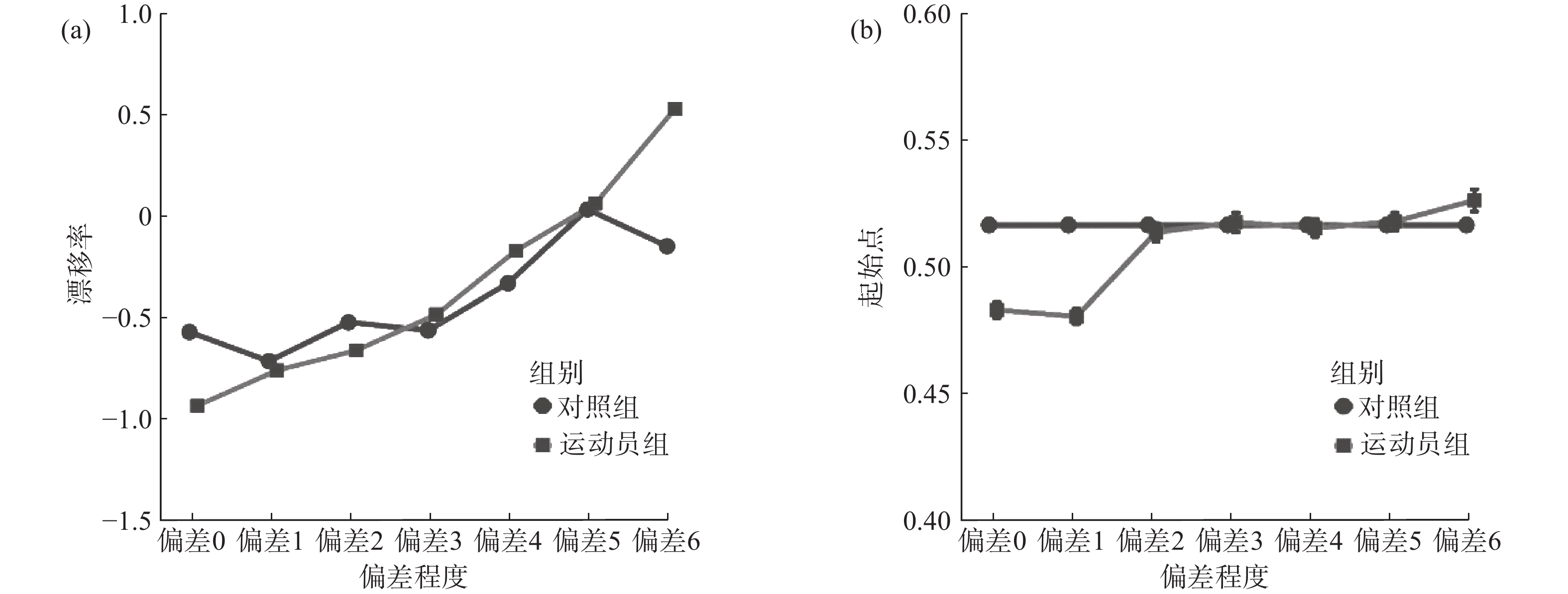
使用组别作为组间因子、偏差程度作为组内因子，通过贝叶斯方差分析对漂移率进行分析。在当前漂移率数据下，包含组别主效应、偏差程度主效应以及组别与偏差程度交互作用的模型优于零模型（$ {\mathrm{B}\mathrm{F}}_{10} $= 1.81×10⁴⁰）和仅包含组别主效应和偏差程度主效应的次优模型（$ {\mathrm{B}\mathrm{F}}_{21} $ = 2.16×10^–41）。如图4（a）所示，随着实际球飞行轨迹与观察到的球飞行轨迹之间偏差程度的增加，漂移率呈正向变化。此外，与其他偏差程度条件相比，运动员组的漂移率在偏差0条件下更为负向，这反映出对“一致”选择边界方向更快的证据累积，而对照组未表现出类似的趋势；与其他偏差程度条件相比，运动员组的漂移率在偏差6条件下更为正向，反映出对“不一致”选择边界的更快的证据累积，而对照组也未表现出类似的趋势。分别对每个偏差程度条件进行贝叶斯独立样本t检验，结果显示，存在极强的证据（extreme evidence）支持运动员组在偏差6条件下有更高的漂移率（$ {\mathrm{B}\mathrm{F}}_{10} $= 410.32），且在偏差0条件下有更低的漂移率（$ {\mathrm{B}\mathrm{F}}_{10} $= 2.07×10⁵）。在其他偏差程度条件下，没有证据（no evidence）或仅有较弱的证据（anecdotal evidence）支持运动员组和对照组之间的漂移率有差异（0.26<$ {\mathrm{B}\mathrm{F}}_{10} $<1.07）。

图  4  运动员组和对照组在各偏差程度条件下的漂移率（a）和起始点（b）

注：对照组的最优模型中起始点不随偏差程度变化而变化。

Figure  4.  Drift rate (a) and starting point (b) across discrepancy conditions and groups

下载: 全尺寸图片 幻灯片

2.3.2   起始点

对于对照组数据，最优模型允许起始点在不同偏差程度条件下自由变化（表2中的模型3），表明对照组在决策过程开始时累积的信息量不受实际球飞行轨迹与观察到的球飞行轨迹之间偏差程度的影响。此外，通过贝叶斯独立样本t检验的方法，检验了对照组的起始点估计值是否与0.5有差异（是否有决策前的倾向），结果显示对照组的起始点偏向“不一致”边界（$ {\mathrm{B}\mathrm{F}}_{10} $= 4.34×10⁵）。

对于运动员组数据，最优模型的起始点随偏差程度变化而变化（表2中的模型5）。将偏差程度作为组内因子，使用贝叶斯方差分析运动员组的起始点参数。包含偏差程度主效应的模型优于零模型（$ {\mathrm{B}\mathrm{F}}_{10} $= 1.10×10⁵³）。如图4（b）所示，随着实际球飞行轨迹与观察到的球飞行轨迹之间偏差程度的增加，起始点向“不一致”边界偏移。分别对每个偏差程度条件下的起始点与0.5进行贝叶斯独立样本t检验，结果显示在偏差0和偏差1条件下运动员组的起始点偏向“一致”边界（$ {\mathrm{B}\mathrm{F}}_{10} $> 8463.23），但在其他条件下运动员组的起始点偏向“不一致”边界（$ {\mathrm{B}\mathrm{F}}_{10} $> 91.25）。

2.3.3   决策阈值和非决策时间

使用贝叶斯独立样本t检验对决策阈值和非决策时间进行分析，结果表明存在中等程度的证据（moderate evidence）支持对照组的决策阈值高于运动员组（$ {\mathrm{B}\mathrm{F}}_{10} $= 4.048），表明对照组需要累积更多的信息量才能做出决策，存在较弱的证据支持运动员组和对照组之间的非决策时间存在差异（$ {\mathrm{B}\mathrm{F}}_{10} $= 1.451）。

3.   分析与讨论

先前的研究^[28−29]已证明运动经验对动作预期偏差监控过程的影响。根据知觉-动作双系统理论，这一过程由负责感知偏差的腹侧通路和负责动作策略调整的背侧通路共同完成，但目前尚未有研究对两者进行分离量化，以探讨运动经验对它们各自的影响。为了填补这一研究空白，采用DDM实现对两者的分离量化，结果显示：①运动员组表现出更高的偏差感知敏感性；②运动员组的起始点受到偏差程度的影响，而对照组不受影响；③运动员组和对照组的漂移率均受到偏差程度的影响，但运动员组的漂移率更为敏感，对偏差程度的变化反应更加细致；④运动员组的决策阈值低于对照组。

3.1   运动经验对偏差感知分级化的影响

在仅考虑全或无的偏差情况下，相比于新手，乒乓球运动员在判断运动学信息和球飞行轨迹信息的一致性方面有更高的敏感性^[5]。然而，近年来有学者^[9]提出，偏差监控系统可能并不是采用全或无的规则，而是采用分级化来表征不同程度的偏差。因此，运动经验对偏差监控的影响可能受到偏差程度的调节。本文引入不同程度偏差，而不是仅考虑全或无的偏差情况。偏差程度越大，偏差感知的难度越小。比较不同偏差条件之间的判定偏差比例差异，这些差异可以反映被试是否采用类似或不同的决策策略来应对不同程度的偏差，结果显示，乒乓球运动员在进行偏差决策时采用了分级化方式，而新手更倾向于采用全或无的方式。例如：面对较小的偏差（偏差1~2），运动员倾向于轻微地调整或修改运动计划；在面对更大偏差（偏差5及以上）时，运动员则可能彻底改变策略以应对显著差异（图2和图3）。这一发现支持了内部模型在感知偏差过程中的关键作用。在人际交互动作中，长期运动经验形成的对专项动作的内部模型使运动员对偏差的感知更为敏感，可以依据偏差程度大小进行动作计划的更新或修改，这种分级化的偏差表征模式极大地提升了快速动作响应的效率^[30]。

3.2   漂移扩散模型视角下运动经验对偏差监控的影响

通过基于决策选择和反应时的DDM，进一步探究运动经验对感知偏差和动作调整策略的影响，结果显示，运动员组的起始点受偏差程度的影响，而对照组不受影响[图4（b）]。具体而言，随着偏差程度的增大，运动员的起始点调整幅度更为显著，表明他们在偏差识别的初期阶段就开始进行策略调整。例如，在偏差0（无偏差）条件下，运动员的决策倾向于保守，起始点向“一致”边界偏移，而在面对显著偏差（如偏差6）时，起始点向“不一致”边界偏移，以调整反应。相比之下，对照组在各种偏差条件下的起始点变化不大，说明他们在偏差识别和策略调整方面的灵活性较低。这表明，乒乓球运动员可以基于内部模型，在观察发球动作和球飞行轨迹后立即感知到偏差，从而促进偏差监控，但由于新手缺乏相应的内部模型，无法迅速对偏差进行编码^[31−32]。此外，运动员基于内部模型形成的偏差感知受到偏差程度的影响。具体而言，运动员在较小偏差程度条件下倾向于 “一致”的决策，而在较大偏差程度条件下则倾向于“不一致”的决策。运动员组和对照组的漂移率均受偏差程度的影响[图4（a）]。与起始点类似，当差异为零（偏差0）或较大（偏差6）时，运动经验影响显著。运动员在偏差为零的条件下表现出更为负向的漂移率，表明与新手相比，运动员更倾向于累积无偏差的证据，进而更快做出“一致”的决策。相反，在较大偏差情况下，运动员表现出更倾向于累积存在偏差证据的反向趋势。这一差异有助于运动员更迅速地调整原有动作计划以应对偏差情况。

上述发现为视觉的知觉-动作双系统理论提供了实证支持^[8]。一方面，运动经验在感知偏差过程中发挥作用，因为只有对特定动作形成了有效的内部模型，才能感知到偏差的存在。另一方面，当偏差感知存在不确定性时，便会进入随后的偏差决策过程。尽管这一加工过程的发生是客观的，但长期运动形成的认知策略会使其具体表达方式呈现经验性分离，即运动员与新手在决策策略上的差异。对于不确定性偏差的处理，运动员在建立特定认知策略方面更为熟练。这些策略包括将视觉资源保留在低确定性目标中，而将运动资源集中用于高确定性目标，以在保证高确定性结果快速响应的同时，降低意外结果造成的不利影响^[15−16]。这种对不确定性的巧妙处理可能有助于运动员在面对预期偏差中的冲突决策时更为灵活，减少偏差决策的风险。

此外，与新手相比，运动员的决策阈值较低，这意味着运动员在做出偏差决策时仅需要较少的证据累积。值得注意的是，两组被试在非决策时间方面没有显著差异，这提示运动经验主要影响了决策过程中的认知加工方式，并未显著影响非决策性认知加工，如按键动作的速度^{[18−19, 22]}。

4.   结 论

基于知觉—动作双系统理论，本文探讨了运动经验对动作预期偏差监控过程的影响，发现运动员在偏差感知方面表现出更高的敏感性。这一优势既源于运动员拥有更完善的内部模型，使其能够更准确地预测动作结果，也源于运动员在面对不确定性偏差时展现出更为灵活的认知策略，特别是在预期偏差的冲突决策方面。这些发现有助于更深入地了解认知加工在动作控制中的关键作用，同时对专业运动员的训练和运动表现提高具有重要应用意义。