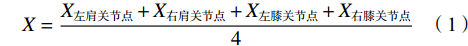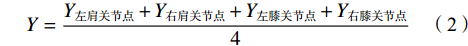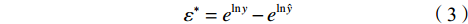A Non-contact Method in Estimating Energy Expenditure in Aerobics Based on OpenPose Algorithm
-
摘要:目的
基于OpenPose计算机视觉算法（以下简称“OpenPose”）获得的运动学参数，构建并验证一种健身操运动能量消耗的非接触式测量方法。
方法通过Qualisys运动捕捉系统验证OpenPose识别关节运动角度的准确性；以COSMED K5便携式气体分析仪测量的能量消耗数据为标准，构建并验证基于OpenPose获得运动学参数的健身操运动能量消耗测量方法。
结果OpenPose能较为准确地估算人体运动中大多数关节的运动角度；基于OpenPose的能量消耗估算方法误差较小（MAE=0.81，MSE=1.11，RMSE=1.02，MRE=13.60%），测试精度可达到86.4%。
结论初步建立了一种基于OpenPose的非接触式能量消耗测量方法，这种新方法能较为准确而简便地测量健身操运动的能量消耗。
-
关键词:
- OpenPose算法 /
- 计算机视觉 /
- 健身操 /
- 能量消耗 /
- 非接触式测量
Abstract:ObjectiveA non-contact method estimating the energy expenditure of aerobics was established and verified based on OpenPose algorithm.
MethodsThe validity of joint angle recognition using OpenPose algorithm was determined with Qualisys motion capture system. Using the energy expenditure measured by COSMED K5 wearable metabolic system as criteria, a novel method based on OpenPose algorithm was established and validated to estimate the energy expenditure of aerobics.
ResultMost joint angles in human movement could be accurately measured by OpenPose algorithm. The error of energy consumption estimation method based on OpenPose computer vision algorithm was fairly good (MAE=0.81, MSE=1.11, RMSE=1.02, MRE=13.60%), and the accuracy could reach 86.4%.
ConclusionA non-contact measurement method of energy consumption in aerobics based on OpenPose algorithm was thus initially established, which could measure the energy consumption in aerobics both accurately and easily.
-
Keywords:
- OpenPose algorithm /
- computer vision /
- aerobics /
- energy expenditure /
- non-contact estimation
-
运动能量消耗是科学健身指导中的关键指标。准确而快速地测量运动能量消耗可量化运动锻炼数据，有助于科学合理地进行能量消耗管理，对于科学健身具有重要意义[1-2]。传统的能量消耗测量方法有双标水法、间接热量测定法、问卷调查法等。前2种方法信效度高，但价格昂贵，使用受限；问卷调查法成本较低，但准确性不高[2]；加速度传感器等可穿戴设备方便智能，可用于能量消耗测量[3]，但该方法须全程佩戴设备，易受外界环境（如竞技比赛、游泳等场景无法佩戴）影响，且效度受个体差异、佩戴位置等因素影响，只在走、跑类项目中表现出较高的精度[4]。
计算机视觉是人工智能正在快速发展的一个分支，采用摄像机等可视化设备代替人眼捕获现实生活中的信息，并通过人工智能分析技术对指定目标进行识别、监测、跟踪及分析[5]。OpenPose计算机视觉算法（以下简称“OpenPose”）是一种开源的多人姿态估计算法，使用者可在单目摄像头的基础上通过OpenPose获得实时且准确率较高的二维人体骨骼关节点坐标[2]。
运动产生的能量消耗由身体质心在水平面的位移做功、身体质心在垂直方向的位移做功、身体的四肢和躯干活动做功、克服阻力做功四部分组成[6]。人体各环节的运动是引起能量消耗增加的重要原因之一，肢体运动的速度和加速度等参数可被用来测量能量消耗[7]。因此，对于在有限范围内进行且无外加负荷的运动，如果能较为准确地捕捉人体各环节的运动学参数，就有望建立一种非接触式新型运动能量消耗测量方法。目前已有部分学者进行了初步探索：Lin等[8]基于计算机视觉技术成功建立了递增负荷跑步机运动的能量消耗模型；Nathan等[9]基于Kinect相机详细探索了上下肢运动、重心变化等关键因素与能量消耗间的关系；Carlson等[10]则将计算机视觉技术应用于学校、公园等场景下的身体活动测量。但上述研究或只针对走跑类和简单肢体运动展开，或只根据运动强度进行能量消耗的分类识别，未能定量地测量能量消耗值。健身操作为一项大众健身运动，活动参与对象范围较广、活动强度适宜且富有趣味，深受群众喜爱。此外，健身操的活动范围固定，适合通过摄像机进行运动数据采集。因此，本文从健身操的能量消耗入手，开展基于计算机视觉算法的能量消耗测量研究，探索实验环境下OpenPose测量人体主要肢体运动的有效性，建立并检验基于OpenPose的健身操运动能量消耗估算方法。
1. 研究方法
基于研究目标，本文开展了2项实验。实验1为OpenPose捕捉关节运动角度的效度验证，实验2为基于OpenPose的健身操能量消耗测量方法的建立与验证。
1.1 OpenPose捕捉关节运动角度的效度验证
通过网络公告方式在浙江大学随机招募10名受试者，其中女性6名、男性4名（表1）。纳入标准为无肢体功能障碍且无皮肤过敏情况。
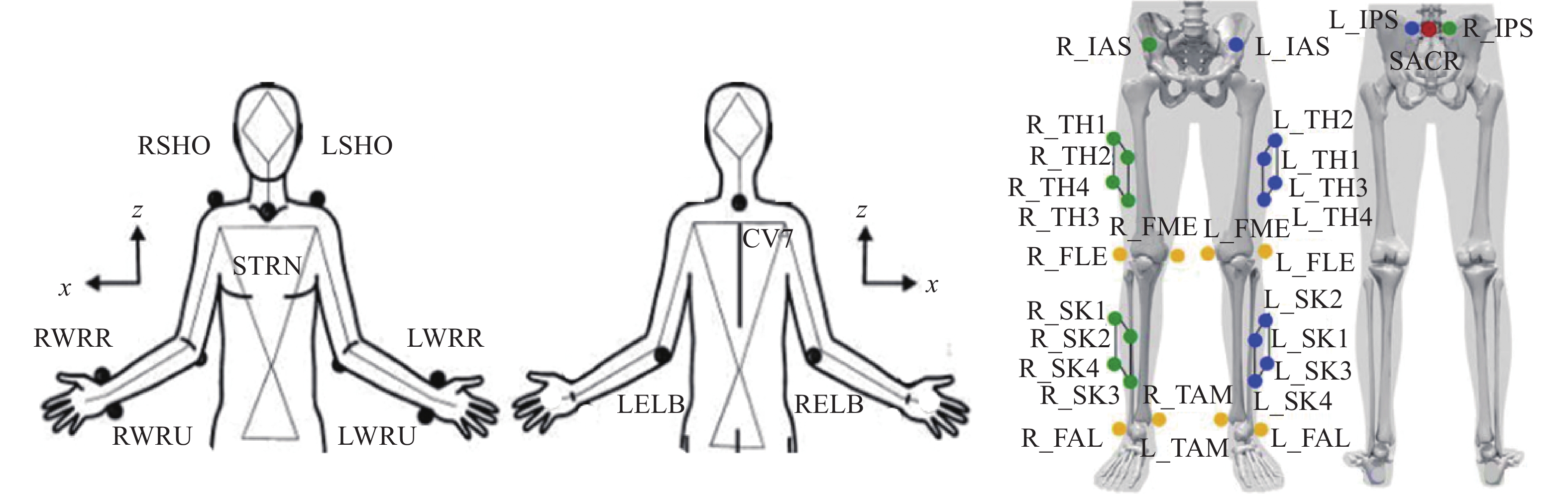
表 1 受试者基本信息（M±SD）Table 1. Descriptive data of subjects基本信息 男性（n=4） 女性（n=6） 年龄/岁 27.8±4.9 26.0±4.6 身高/cm 170.5±3.8 166.6±6.0 体质量/kg 64.25±8.2 58.3±4.9 BMI/(kg·m−2) 22.1±2.7 21.0±0.9 实验在装有Qualisys Oqus7+三维运动分析系统的实验室进行，室内有1台用于同步拍摄的智能手机。Qualisys可以跟踪记录粘贴在人体体表反光点的运动轨迹，拍摄帧率为200 Hz，手机的拍摄帧率为30 Hz，二者全程进行拍摄记录，上肢和下肢的反光点粘贴方式如图1所示。
受试者全身粘贴39个反光点，完成7个关节运动。分别为在冠状面内进行的肩关节和髋关节外展，以及在矢状面内进行的肘关节、肩关节、膝关节和髋关节屈曲运动。完成外展运动时，受试者正面正对相机，后需向左旋转90°，使右侧面正对相机完成各关节的屈曲运动（图2）。
1.1.1 测试指标
（1）基于Qualisys系统的运动指标。将Qualisys捕捉到的39个反光点数据导入Visual 3D三维运动分析软件，创建CODA骨盆模型、上肢模型、下肢模型和躯干模型，得到研究适用的人体骨架模型。输入受试者的身高、体质量信息完成模型的应用，分析得到肩、肘、髋、膝关节的关节角度数据，作为运动指标的标准值。
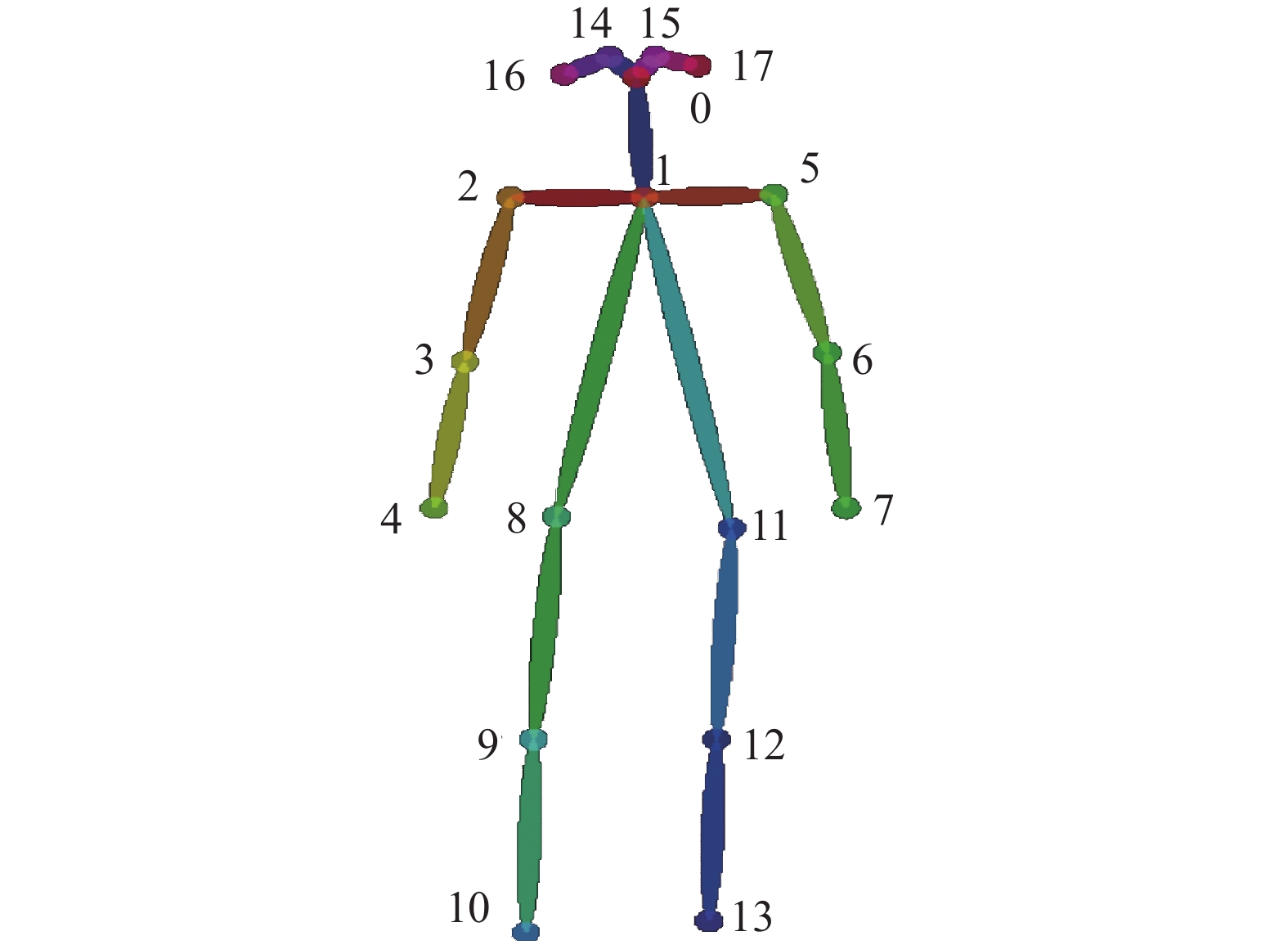
（2）基于OpenPose的运动指标。使用OpenPose识别手机拍摄视频中的人体骨架，提取关节点的坐标[11]。OpenPose是一种自底而上的人体姿态估计算法，即先找到人体特征部位，得到关节位置置信图，再连接骨骼，组合人体。一张三原色（RGB）图片首先经一个卷积神经网络处理，生成特征图，之后特征图被输入双分支网络，得到关节点置信度图S和人体部分亲和字段L。置信度数值最大处为预测关节点所在位置，人体部分亲和字段同时保留了肢体的位置和方向信息。由此可通过比较任意2个关节点的连线与人体部分亲和字段中对应线段的对齐程度选择正确的连接方式，形成人体骨架[12]。本文选取图3中编号为1—13的13个关节点，计算得到肩、肘、髋、膝各关节的关节角度，作为运动指标的检测值。
1.1.2 统计分析
采用SPSS 22.0软件对数据进行统计分析。通过Spearman相关分析检验基于Qualisys系统的运动指标标准值和基于OpenPose的运动指标检测值的相关性。通过组内相关系数（Intraclass Correlation Coefficient，ICC）检验测量结果的一致性。2种方法得到的数据差异以平均绝对值误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）和平均相对误差（Mean Relative Error，MRE）表示，单位为度（°），数值越小说明2组数据越一致。
相关分析结果范围在0.80～1.00表示极强相关，0.60～0.79表示强相关，0.40～0.59表示中等程度相关，0.20～0.39表示弱相关，0～0.19表示极弱相关或无相关[8]。组内相关系数小于0.4表示一致性较差，大于0.75表示一致性良好。P<0.05表示具有显著性差异，P<0.01表示具有非常显著性差异，P<0.001表示具有极显著性差异。
1.2 基于OpenPose的健身操能量消耗测量方法的建立与验证
以网络广告方式随机招募20名受试者，均为女性（表2）。纳入标准：①1个月内无明显体质量减轻，饮食正常；②无心肺功能异常；③无代谢性疾病；④无肢体功能障碍；⑤BMI属于正常水平；⑥年龄在20～30岁；⑦不佩戴框架眼镜（避免因眼镜问题影响呼吸面罩的佩戴）；⑧有规律锻炼习惯。实验前3 h受试者不得进食、吸烟或进行中高强度运动，实验前12 h不得摄入任何含咖啡因的饮品，实验前一晚保证至少7 h的充足睡眠。测量并记录受试者的基本信息，所有受试者需签署知情同意书并自愿参加此次实验。
表 2 受试者基本信息（M±SD）Table 2. Descriptive data of subjects基本信息 女性（n=20） 年龄/岁 23.0±2.1 身高/cm 164.5±6.5 体质量/kg 54.9±6.1 BMI/（kg·m−2） 20.2±1.2 体脂率/% 23.5±3.1 腰围/cm 68.1±4.7 腿长/cm 89.5±4.4 注：腿长的测量以髂前上棘为起点、内踝为终点。 受试者穿戴好已校验的Cosmed K5（Cosmed，Rome，Italy）便携式气体分析仪和配套心率带，静坐3～5 min，记录下降至稳态的心率作为静息心率。随后完成一套由15个不同动作组成的健身操，动作涵盖了大众健身操各关节的主要运动形式。动作选择的依据：①涵盖主要关节的主要运动形式；②被广泛采纳的健身操中的常用动作，至少在2个以上网络热度较高的健身操中出现过；③动作难度适宜，普通人都可以完成，保证实验的可行性；④控制总量，避免因受试者过于疲劳影响测量效果，动作总数控制在15个；⑤根据预实验能量消耗结果，按照运动强度从低到高排序，避免相互干扰。每个动作持续3 min，不同动作间以30 s的踏步作为过渡动作，健身操总时长为52.5 min。受试者的正前方、正左侧和正右侧各放置1台智能手机完成全程记录。实验1仅对矢状面和冠状面内的关节活动角度进行验证，故所有动作的主要运动平面为冠状面或矢状面。
1.2.1 测试指标
（1）能量消耗指标。Cosmed K5便携式气体分析仪导出的数据每10 s记录1次，选用每个动作最后1 min达到稳态时的相对摄氧量[mL/（min·kg）][13]，除以静息代谢的摄氧量3.5 [mL/（min·kg）]并取均值，得到各个动作的平均梅脱值（Metabolic Equivalent，MET），作为能量消耗指标。
（2）心率相关指标。GARMIN心率带每10 s记录1次数据，20名女性受试者的静息心率为（70.0±9.7）次/min。选用每个动作最后1 min达到稳态时的心率作为心率指标，并基于最大心率、静息心率和当前动态心率计算得到心率储备百分比（Percentage of Heart Rate Reserve，%HRR）指标。上述2个指标均取平均值作为心率相关指标。
（3）基于OpenPose的运动指标。除实验1中的运动指标外，实验2中还加入了躯干的运动角度和用于模拟重心位置变化的身体中心点在竖直和水平方向的运动参数。各关节角度通过3个连接点的坐标换算得到。身体中心点横纵坐标的计算方式如下：
$$ X=\dfrac{{X}_{左肩关节点}+{X}_{右肩关节点}+{X}_{左膝关节点}+{X}_{右膝关节点}}{4} $$ (1) $$ Y=\dfrac{{Y}_{左肩关节点}+{Y}_{右肩关节点}+{Y}_{左膝关节点}+{Y}_{右膝关节点}}{4} $$ (2) 基于关节角度，计算得到角速度和角加速度，以及身体中心点的移动速度和加速度。取每个动作最后1 min达到稳态时的数据，以平均值和标准差表示，该部分数据是实验2的运动指标。各关节对应连接点和拍摄视角如表3所示。
表 3 关节构造示意Table 3. Method of joint connection关节名称 连接点 拍摄视角 左肩关节 1—5—6 正面 右肩关节 1—2—3 正面 左肘关节 5—6—7 正面/侧面 右肘关节 2—3—4 正面/侧面 左髋关节 5—11—12 正面/侧面 右髋关节 2—8—9 正面/侧面 左膝关节 11—12—13 正面/侧面 右膝关节 8—9—10 正面/侧面 左肩关节 6—5—11 侧面 右肩关节 3—2—8 侧面 躯干 1—8—9 正面/侧面 1.2.2 统计分析
采用SPSS 22.0软件对数据进行统计分析。通过Spearman相关分析检验能量消耗指标与能量消耗测量指标（共计130个），包括：运动指标（121个），如右膝关节角速度均值；个人基本信息指标（7个），如身高；心率均值和%HRR平均值的相关性。保留相关系数大于0.2（P<0.05）的指标，进行逐步回归分析，通过决定系数（R2）判断拟合程度，建立3个回归模型。采用10折交叉验证方法（10-fold Cross Validation）[14-15]得到各模型的平均绝对值误差、均方误差（Mean Square Error, MSE）、均方根误差[8, 16]和平均相对误差[17]，用以评价模型的测量准确性。
2. 研究结果
2.1 基于OpenPose捕捉关节运动角度变化情况
2.1.1 关节运动角度变化趋势
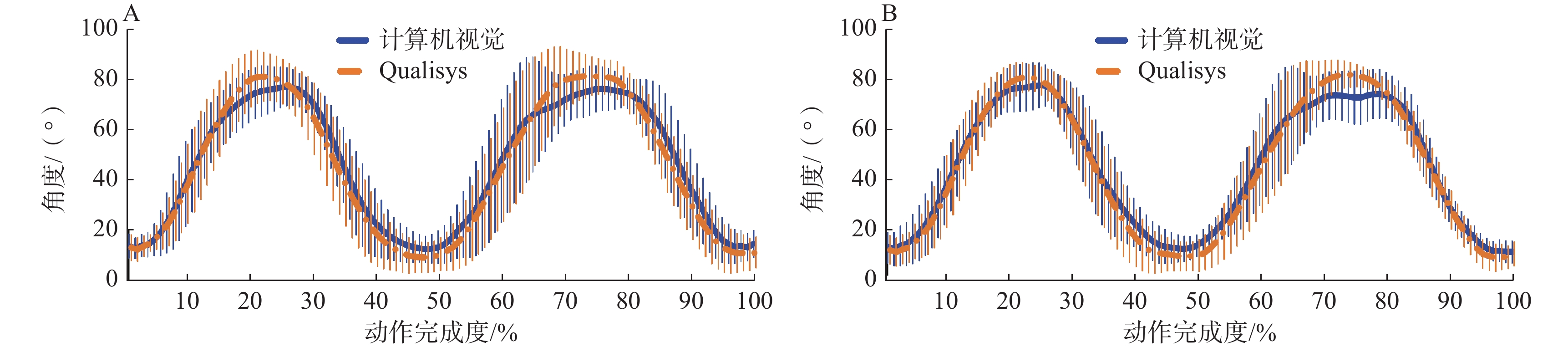
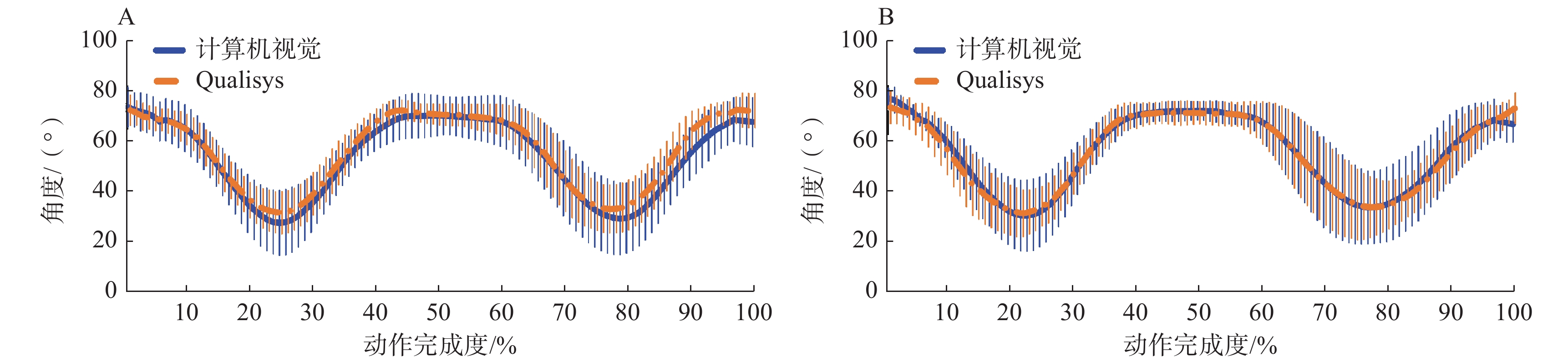
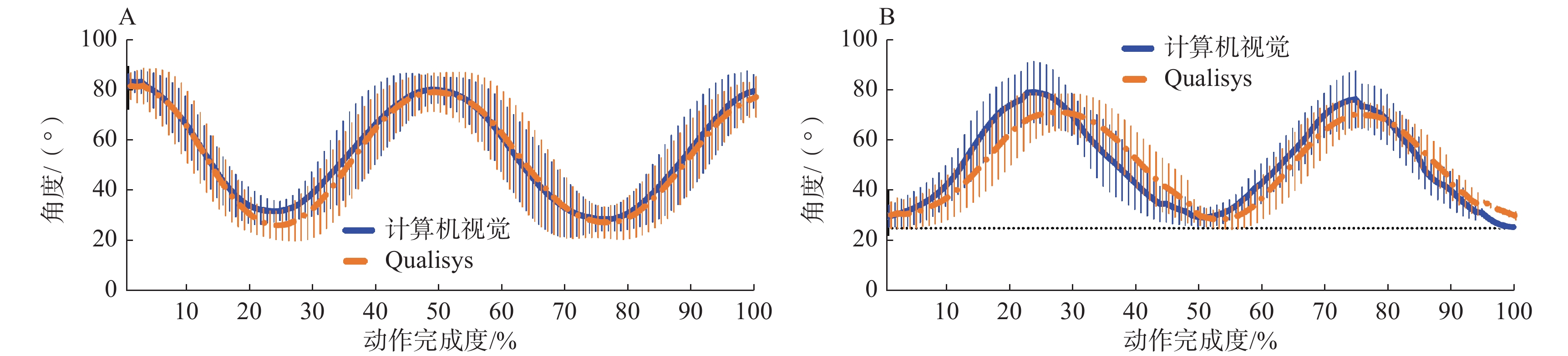
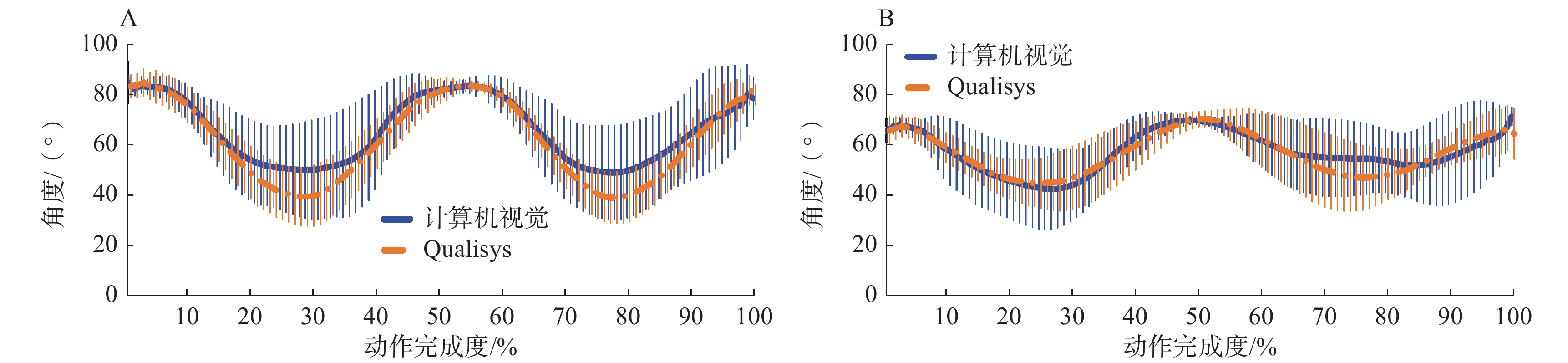
所有受试者的关节运动角度以平均值和标准差的形式表示。图4和图5分别为正面相机拍摄的肩关节和髋关节在冠状面做外展运动的角度变化曲线，图6和图7分别为右侧相机拍摄的右肘、右肩、右膝和右髋关节在矢状面做屈曲运动的角度变化曲线。
![]()
图 4 左肩关节（A）和右肩关节（B）外展运动角度变化曲线注：图中曲线表示平均值，阴影部分表示标准差。Figure 4. Angle changes of left (A) and right (B) shoulder joints during abduction![]()
图 5 左髋关节（A）和右髋关节（B）外展运动角度变化曲线注：图中曲线表示平均值，阴影部分表示标准差。Figure 5. Angle changes of left (A) and right (B) hip joints during abduction![]()
图 6 右肘关节（A）和右肩关节（B）屈曲运动角度变化曲线注：图中曲线表示平均值，阴影部分表示标准差。Figure 6. Angle changes of right elbow (A) and shoulder (B) joints during buckling![]()
图 7 右膝关节（A）和右髋关节（B）屈曲运动角度变化曲线注：图中曲线表示平均值，阴影部分表示标准差。Figure 7. Angle changes of right knee (A) and hip (B) joints during buckling结果显示：2种方法得到的关节运动角度均值曲线和标准差变化趋势基本一致，角度峰值处存在一定误差；相较于侧面拍摄的屈曲运动，正面拍摄的外展运动均值曲线更加一致；下肢关节做屈曲运动时的角度波动范围较其他情况更大。
2.1.2 关节运动角度的相关分析和一致性分析
关节运动角度的相关分析和一致性分析结果（表4）显示，Qualisys系统和OpenPose得到的各关节运动角度均极强相关（r>0.8），且一致性结果良好（ICC>0.75）。相较于髋关节，肩关节的相关系数更加稳定，且上肢关节的相关系数普遍高于下肢关节。
表 4 相关分析和一致性分析结果Table 4. Results of correlation analysis and interclass correlation analysis关节名称 运动类型 拍摄位 r ICC 左肩关节 外展 正面 0.922*** 0.879*** 右肩关节 外展 正面 0.929*** 0.869*** 左髋关节 外展 正面 0.819*** 0.948*** 右髋关节 外展 正面 0.914*** 0.953*** 右肘关节 屈曲 侧面 0.961*** 0.927*** 右肩关节 屈曲 侧面 0.924*** 0.849*** 右膝关节 屈曲 侧面 0.875*** 0.948*** 右髋关节 屈曲 侧面 0.893*** 0.869*** 注：*表示P<0.05，**表示P<0.01，***表示P<0.001。 2.1.3 关节运动角度测量误差分析
关节运动角度测量误差分析结果（表5）显示，正面拍摄的关节运动角度误差普遍小于侧面，同一关节左右侧误差相近，侧面拍摄的膝关节屈曲运动误差最大。
表 5 关节运动角度测量误差Table 5. Errors of joint angle关节名称 运动类型 拍摄位 MAE/（°） RMSE/（°） MRE/% 左肩关节 外展 正面 6.85 9.12 21.52 右肩关节 外展 正面 6.54 8.59 20.99 左髋关节 外展 正面 5.34 7.61 4.30 右髋关节 外展 正面 5.11 7.24 3.45 右肘关节 屈曲 侧面 7.79 11.01 9.64 右肩关节 屈曲 侧面 9.07 16.97 24.26 右膝关节 屈曲 侧面 15.67 21.54 18.85 右髋关节 屈曲 侧面 7.83 12.93 14.18 2.2 基于OpenPose的健身操能量消耗测量方法构建
2.2.1 健身操能量消耗测量结果
本文所选健身操由15个不同动作组合而成，各动作实测能量消耗（表6）近似于一项逐级递增负荷运动，属于中至高等强度运动。
表 6 健身操各动作的心率、代谢当量和呼吸商（M±SD）Table 6. Heart rate，METS and respiratory quotient of aerobics动作序号 心率/（次·min−1） 代谢当量/METs 呼吸商 1 99.2±14.6 4.0±0.7 0.83±0.069 2 110.8±16.7 5.2±1.0 0.82±0.054 3 109.1±14.6 5.0±0.9 0.89±0.061 4 117.7±17.0 5.1±0.9 1.00±0.080 5 117.7±16.9 5.0±1.0 0.96±0.057 6 128.9±18.9 5.0±1.2 0.96±0.082 7 119.6±19.1 4.9±0.7 0.93±0.059 8 124.1±17.3 5.5±1.1 0.99±0.067 9 127.7±17.8 5.9±1.2 0.87±0.057 10 122.9±18.3 6.2±1.1 0.88±0.040 11 138.1±18.5 6.7±1.2 0.93±0.064 12 137.9±16.4 7.2±1.2 0.85±0.044 13 137.6±18.4 6.7±1.3 0.90±0.052 14 143.4±17.4 7.0±1.1 0.88±0.047 15 153.9±15.3 8.4±1.5 0.92±0.059 2.2.2 关节运动学参数与能量消耗的相关分析
本文保留了60个相关系数大于0.2（P<0.05）的能量消耗测量指标（58个运动指标，2个心率指标），其中身体中心、躯干及下肢关节运动指标的相关系数相对较高，相同关节左右两侧相机拍摄所得相关系数相近，侧面拍摄所得运动指标的相关系数普遍大于正面拍摄。除运动指标外，心率与%HRR显示出与能量消耗的强相关性，身体中心指标在竖直方向的运动变量与能量消耗中等程度相关。
2.2.3 能量消耗测量模型
将相关分析后保留的58个运动指标分为3组，分别为正面拍摄指标组、侧面拍摄指标组、正面加侧面拍摄指标组。以各组的运动指标为自变量，能量消耗指标为因变量，经逐步回归筛选得到3个能量消耗测量模型。由于心率相关变量与能量消耗指标存在强相关性，在上述3个模型中依次分别加入心率和%HRR变量，观察模型决定系数的变化。根据模型分析结果（表7）发现，%HRR变量能更好地提升模型的测量能力，因此选定该变量为辅助变量，分别加入上述3个模型。因能量消耗指标不服从正态分布，将上述所有指标经自然对数转换后再展开分析。
表 7 能量消耗测量模型基本信息Table 7. Basic information of energy consumption measurement models模型 调整后R2 SEE 自变量名称 自变量释义 β1 β2 VIF 模型 1 0.387 0.203 常数 — 0.703 — — AVE_KNR_FA 正面右膝角加速度均值 −0.309 −0.457 10.315 SD_KNR_FA 正面右膝角加速度标准差 0.364 0.643 9.927 SD_YV 身体中心纵向运动速度标准差 0.235 0.576 1.127 模型 2 0.541 0.174 常数 — 1.452 — — AVE_SHL_L 侧面左肩角度均值 0.050 0.132 2.502 AVE_ELR_R 侧面右肘角度均值 0.110 0.101 1.138 AVE_HIPL_LV 侧面左髋角速度均值 0.190 0.410 2.860 AVE_KNL_L 侧面左膝角度均值 0.960 0.267 2.955 AVE_KNR_RA 侧面右膝角加速度均值 0.130 0.219 1.547 AVE_TR_R 侧面躯干角度均值 −1.502 −0.395 2.487 SD_SHR_R 侧面右肩角度标准差 0.049 0.137 2.386 模型 3 0.628 0.158 常数 — 0.051 — — AVE_SHL_LV 侧面左肩角速度均值 0.079 0.211 1.114 AVE_HIPL_LV 侧面左髋角速度均值 0.090 0.191 3.413 AVE_KNR_RA 侧面右膝角加速度均值 0.195 0.326 3.168 AVE_TR_RV 侧面躯干角速度均值 0.158 0.314 5.500 AVE_YA 身体中心纵向运动加速度均值 −0.291 −0.665 7.193 SD_KNR_R 侧面右膝角度标准差 −0.122 −0.249 2.599 SD_YV 身体中心纵向运动速度标准差 0.362 0.893 6.111 注：β1表示非标准化系数，β2表示标准化系数。 在表7中：模型1的自变量除常数项外均为正面拍摄的运动指标，分别为右膝角加速度均值与标准差，以及身体中心纵向运动速度标准差；模型2的自变量除常数项外均为侧面拍摄的运动指标，分别为左肩、左膝、右肘、躯干的角度均值，左髋角速度均值，右膝角加速度均值以及右肩角度标准差；模型3的自变量除常数项外为正面加侧面拍摄的运动指标，分别为左肩、左髋、躯干的角速度均值，右膝角加速度均值，身体中心纵向运动的加速度均值和速度标准差，以及右膝角度标准差。结果显示：各模型都纳入了膝关节的运动指标；模型中下肢关节运动指标占比高于上肢关节；可获得身体中心指标的模型都纳入了该指标作为自变量；根据决定系数由低至高排序为模型1（R2=0.387）<模型2（R2=0.541）<模型3（R2=0.628）。加入%HRR后，3个模型的决定系数均得到提升，但依然表现为模型1-1（R2=0.557）<模型2-1（R2=0.655）<模型3-1（R2=0.696）。
2.2.4 模型测量准确性结果
由于建模前所有变量均经过自然对数转换，需通过式（3）计算得到实测代谢当量与模型测量代谢当量的差值，即测量误差ε*，单位为METs。经交叉检验得到各误差检验指标，具体操作为：将20名受试者随机分成10组，每组2人。每次利用其中9组的数据作为建模组，分别构建上述6个模型的能量消耗测量方程。剩余1组作为回代验证组，计算得到代谢当量的测量值，由此可以得到实际测量值与方程测量值的差值，即为测量误差。重复这个过程直到每组数据都曾作为独立的实际观测值完成与模型测量值的比较。
$${\varepsilon ^*} = {e^{\ln y}} - {e^{\ln \hat y}} $$ (3) 模型测量误差结果（表8）显示，基于运动指标的模型1、模型2、模型3有较好的测量准确度，平均绝对值误差均小于1.0 METs。加入%HRR后，各模型的测量准确性得到了不同程度的优化。
表 8 模型测量误差结果Table 8. Error results of models误差指标 模型1 模型1-1 模型2 模型2-1 模型3 模型3-1 MAE/METs 0.96 0.84 0.89 0.76 0.81 0.74 MSE/METs 1.53 1.16 1.36 1.00 1.11 0.91 RMSE/METs 1.19 0.97 1.14 0.96 1.02 0.92 MRE/% 17.14 14.80 15.13 12.90 13.60 12.33 注：模型1基于正面运动指标建立，模型2基于侧面运动指标建立，模型3基于正面和侧面运动指标建立，模型1-1、模型2-1和模型3-1分别在模型1、2、3的基础上加入了%HRR。 对比相关研究发现，与使用能获取三维数据的深度相机研究[8]相比，本文测量结果的误差稍高。这既可能因为Lin等[8]的研究对象为简单跑步运动，也可能因为深度相机能获取更高精度的人体骨架三维数据。与基于多个惯性传感器和心率设备，以日常活动、锻炼活动等同样较为复杂的混合类活动为对象的研究[18-19]相比，模型测量的误差结果并无较大差异。但本文的实验无须佩戴任何设备，使用更加方便。
3. 讨 论
基于OpenPose得到的关节运动指标与健身操运动的能量消耗存在相关性。关节活动是人体运动的可视化表现，在增加生理能耗的同时对外做功。关节运动的角度在一定程度上代表了运动范围，关节运动的角速度和角加速度代表了运动强度，均为人体能量消耗的影响因素。相关研究[7, 20-23]已证实身体活动的速度和加速度与摄氧量、能量消耗之间的关系，为本文提供了一定的支撑。本文结果也显示，通过计算机视觉采集人体运动参数，并间接测量人体运动能量消耗是可行的。本文所使用的研究方法存在12%～17%的误差，这与测量能量消耗的主流智能设备（如Actigraph加速度计等30%左右的误差[24]、Fitbit等智能手环20%～35%的误差）[25]相比存在一定优势，可能具有较好的应用前景。
3.1 基于OpenPose的关节运动参数识别精度
基于OpenPose的人体关节角度识别精度因运动关节和拍摄面的不同存在差异。首先，基于OpenPose得到的人体骨架模型与人体真实骨架结构存在偏差（图3）。如表3所示，基于二维模型的左右髋关节以左右髂前上棘点（点11和点8）为关节中心，与两肩峰点（点5和点2）和左右膝关节点（点12和点9）连线构成，无法还原骨盆的立体结构，且这种跨关节的连接方式更容易造成数据误差和数据缺失。其次，关节角度识别的准确度因拍摄视角不同存在偏差。使用手机拍摄的RGB视频不具备视角不变性，对光线和背景变化都很敏感[26]。实验室环境可减少光线与背景的影响，但仍无法实现视角不变性，容易影响分析效果。此外，相较于正面拍摄，侧面拍摄视角下，肢体、躯干之间的相互遮挡易导致识别误差。例如，相机位于侧面时，左右膝关节点几乎重叠，图3中关节点1也很难被正确估算。膝关节的主要运动形式为屈伸运动，在矢状面内进行，这会影响膝关节角度的识别精度。相关研究结果显示，OpenPose对人体膝关节点的检验精度较肩、肘、髋关节点更低[11]，同样用于人体姿势识别的AlaphaPose对膝关节点的检测精度要比OpenPose高11%[12]。
3.2 不同拍摄面运动指标与能量消耗的关系
在关节角度识别精度低于正面的情况下，侧面拍摄的屈伸类活动的运动指标仍更适合测量能量消耗。表现为侧面指标与能量消耗的相关性较正面指标更高，模型2的决定系数（R2=0.541）较模型1（R2=0.387）更高，模型2的误差较模型1更低。从解剖学角度分析，实验中侧面相机记录的是人体各关节在矢状面内进行的屈伸类运动，正面相机记录的则是在冠状面内进行的外展内收类运动。行走、跑步、爬楼梯等活动的主要运动平面都为矢状面，屈伸类活动为主要日常活动。骨骼肌收缩时的肌力大小和沿力方向的位移对能量消耗产生影响。肌力的大小取决于被激活运动单位的类型、数量、刺激频率等[27]，同时根据关节功率法，肌肉在某关节做功的功率由关节合力矩与关节角度的乘积共同决定[28]。因此相较于展肌和收肌，经常作为主要运动肌的屈肌和伸肌的肌力更大，伸展性与弹性更佳，从而运动幅度也更大，对能量消耗产生更大的影响。健身操中能量消耗较高的几个动作的主要运动平面均为矢状面。
3.3 上下肢关节运动指标与能量消耗的关系
相较于上肢关节，下肢关节即使存在一定测量误差，其运动指标仍在能量消耗测量方程中起到更重要的作用。因直立行走，人类下肢肌肉较上肢肌肉更为发达，占全身肌肉重量的比例更高[29]。日常生活中上肢肌肉的活动时间、频率、频次都大于下肢肌肉，但下肢肌肉单次的收缩幅度远大于上肢肌肉[30]。相关研究[31-32]证实，在不同的运动角度、运动速度以及外加负荷下，上肢关节活动导致的能量消耗较低。另有研究[33]发现，与上肢活动主导的游戏相比，下肢活动主导的游戏的平均能量消耗要高出6倍之多，下肢活动在能量消耗中起主要作用。健身操运动需要参与者随音乐律动，通常是全身性活动，尤其是下肢活动。本文所选健身操的15个动作均含下肢运动，且下肢关节运动角度较大的动作，实测能量消耗也更多。
3.4 身体中心指标与能量消耗的关系
身体中心指标的垂直变量与能量消耗存在一定关系。能量消耗可分为用于移动身体重心的部分和相对于身体重心移动的四肢部分[34]，身体中心指标意在表征身体重心的运动轨迹。在没有外加负重的情况下，身体主要通过下肢和躯干肌肉的收缩作用克服重力做功。重力作用的方向可视为恒定不变，功的大小主要由人体重心在竖直方向的位移决定。因腰部最接近人体的重心位置，在腰部佩戴加速度计是测量身体活动较为推荐的方式[35]。美国运动医学会推荐的走跑类运动的摄氧量测量公式显示，坡度与摄氧量呈正相关[36]，即在相同的运动速度下，坡度越高，克服重力做功越多，摄氧量越高，能量消耗越大，能量消耗与重心的垂直变化有关。本文健身操运动以能量消耗由低至高的方式进行动作排序，实验后期有较为明显的下蹲动作，重心位置在竖直方向上的变化逐渐增强，因此实测能量消耗值更高。
3.5 %HRR与能量消耗的关系
在能量消耗测量模型中加入%HRR指标可优化模型的测量结果。心率与耗氧量存在线性关系[26]，心率结合运动传感器测量有氧运动能量消耗的技术已得到成熟应用[22, 37]。心率表现存在个体差异，例如有一定训练基础的人，其安静心率往往低于不经常运动的人，在运动时也具有更大的提升空间。以心率储备代替心率能在一定程度上减轻个体差异的影响，提高能量消耗测量模型的准确性[38]。早期有学者[39]使用%HRR评估久坐妇女的训练强度，最新的《ACSM运动测试与运动处方指南》已经推荐用%HRR评估有氧运动的适宜强度[40]。%HRR在身体活动相关研究中逐渐得到较为广泛的应用[41-42]。健身操运动作为一种大众健身活动，对参与人员的体适能状况没有特殊要求，因此参与者的心率反应受个体差异影响较大，更适合采用心率储备指标。
综上，在不佩戴任何设备的情况下，基于正面和侧面运动指标的模型3能较好地估算复杂运动情况下人体的能量消耗，具有较高应用价值。心率传感器可作为辅助设备以提高该方法的精度，但效果有限。
4. 结 论
OpenPose能构建人体骨架模型，连续跟踪记录运动过程中的各关节角度。上肢关节角度的误差结果比下肢关节更稳定。正面识别的关节角度误差小于侧面。基于OpenPose的能量消耗估算新方法误差较小（MAE=0.81，MSE=1.11，RMSE=1.02，MRE=13.60%），测试精度可达到86.4%。本文初步建立了一种基于OpenPose的健身操能量消耗非接触式测量方法，这种新方法能较为准确、简便地测量健身操锻炼中的能量消耗，未来有望发展为运动能量消耗测量的重要方法。
作者贡献声明：温煦：提出论文主题，设计论文框架，撰写论文，审核、指导并修改论文；作者贡献声明：杨雨馨：检索文献，招募受试者，采集、分析数据，撰写论文；作者贡献声明：高元龙：招募受试者；作者贡献声明：李宽：采集数据；作者贡献声明：杨建党：筛选、分析数据；作者贡献声明：杨小倩：筛选、提取资料；作者贡献声明：刘勇：核实统计数据与结果，指导论文。 -
![]()
图 4 左肩关节（A）和右肩关节（B）外展运动角度变化曲线
注：图中曲线表示平均值，阴影部分表示标准差。
Figure 4. Angle changes of left (A) and right (B) shoulder joints during abduction
![]()
图 5 左髋关节（A）和右髋关节（B）外展运动角度变化曲线
注：图中曲线表示平均值，阴影部分表示标准差。
Figure 5. Angle changes of left (A) and right (B) hip joints during abduction
![]()
图 6 右肘关节（A）和右肩关节（B）屈曲运动角度变化曲线
注：图中曲线表示平均值，阴影部分表示标准差。
Figure 6. Angle changes of right elbow (A) and shoulder (B) joints during buckling
![]()
图 7 右膝关节（A）和右髋关节（B）屈曲运动角度变化曲线
注：图中曲线表示平均值，阴影部分表示标准差。
Figure 7. Angle changes of right knee (A) and hip (B) joints during buckling
表 1 受试者基本信息（M±SD）
Table 1 Descriptive data of subjects
基本信息 男性（n=4） 女性（n=6） 年龄/岁 27.8±4.9 26.0±4.6 身高/cm 170.5±3.8 166.6±6.0 体质量/kg 64.25±8.2 58.3±4.9 BMI/(kg·m−2) 22.1±2.7 21.0±0.9 
下载: 导出CSV
表 2 受试者基本信息（M±SD）
Table 2 Descriptive data of subjects
基本信息 女性（n=20） 年龄/岁 23.0±2.1 身高/cm 164.5±6.5 体质量/kg 54.9±6.1 BMI/（kg·m−2） 20.2±1.2 体脂率/% 23.5±3.1 腰围/cm 68.1±4.7 腿长/cm 89.5±4.4 注：腿长的测量以髂前上棘为起点、内踝为终点。
下载: 导出CSV
表 3 关节构造示意
Table 3 Method of joint connection
关节名称 连接点 拍摄视角 左肩关节 1—5—6 正面 右肩关节 1—2—3 正面 左肘关节 5—6—7 正面/侧面 右肘关节 2—3—4 正面/侧面 左髋关节 5—11—12 正面/侧面 右髋关节 2—8—9 正面/侧面 左膝关节 11—12—13 正面/侧面 右膝关节 8—9—10 正面/侧面 左肩关节 6—5—11 侧面 右肩关节 3—2—8 侧面 躯干 1—8—9 正面/侧面
下载: 导出CSV
表 4 相关分析和一致性分析结果
Table 4 Results of correlation analysis and interclass correlation analysis
关节名称 运动类型 拍摄位 r ICC 左肩关节 外展 正面 0.922*** 0.879*** 右肩关节 外展 正面 0.929*** 0.869*** 左髋关节 外展 正面 0.819*** 0.948*** 右髋关节 外展 正面 0.914*** 0.953*** 右肘关节 屈曲 侧面 0.961*** 0.927*** 右肩关节 屈曲 侧面 0.924*** 0.849*** 右膝关节 屈曲 侧面 0.875*** 0.948*** 右髋关节 屈曲 侧面 0.893*** 0.869*** 注：*表示P<0.05，**表示P<0.01，***表示P<0.001。
下载: 导出CSV
表 5 关节运动角度测量误差
Table 5 Errors of joint angle
关节名称 运动类型 拍摄位 MAE/（°） RMSE/（°） MRE/% 左肩关节 外展 正面 6.85 9.12 21.52 右肩关节 外展 正面 6.54 8.59 20.99 左髋关节 外展 正面 5.34 7.61 4.30 右髋关节 外展 正面 5.11 7.24 3.45 右肘关节 屈曲 侧面 7.79 11.01 9.64 右肩关节 屈曲 侧面 9.07 16.97 24.26 右膝关节 屈曲 侧面 15.67 21.54 18.85 右髋关节 屈曲 侧面 7.83 12.93 14.18
下载: 导出CSV
表 6 健身操各动作的心率、代谢当量和呼吸商（M±SD）
Table 6 Heart rate，METS and respiratory quotient of aerobics
动作序号 心率/（次·min−1） 代谢当量/METs 呼吸商 1 99.2±14.6 4.0±0.7 0.83±0.069 2 110.8±16.7 5.2±1.0 0.82±0.054 3 109.1±14.6 5.0±0.9 0.89±0.061 4 117.7±17.0 5.1±0.9 1.00±0.080 5 117.7±16.9 5.0±1.0 0.96±0.057 6 128.9±18.9 5.0±1.2 0.96±0.082 7 119.6±19.1 4.9±0.7 0.93±0.059 8 124.1±17.3 5.5±1.1 0.99±0.067 9 127.7±17.8 5.9±1.2 0.87±0.057 10 122.9±18.3 6.2±1.1 0.88±0.040 11 138.1±18.5 6.7±1.2 0.93±0.064 12 137.9±16.4 7.2±1.2 0.85±0.044 13 137.6±18.4 6.7±1.3 0.90±0.052 14 143.4±17.4 7.0±1.1 0.88±0.047 15 153.9±15.3 8.4±1.5 0.92±0.059
下载: 导出CSV
表 7 能量消耗测量模型基本信息
Table 7 Basic information of energy consumption measurement models
模型 调整后R2 SEE 自变量名称 自变量释义 β1 β2 VIF 模型 1 0.387 0.203 常数 — 0.703 — — AVE_KNR_FA 正面右膝角加速度均值 −0.309 −0.457 10.315 SD_KNR_FA 正面右膝角加速度标准差 0.364 0.643 9.927 SD_YV 身体中心纵向运动速度标准差 0.235 0.576 1.127 模型 2 0.541 0.174 常数 — 1.452 — — AVE_SHL_L 侧面左肩角度均值 0.050 0.132 2.502 AVE_ELR_R 侧面右肘角度均值 0.110 0.101 1.138 AVE_HIPL_LV 侧面左髋角速度均值 0.190 0.410 2.860 AVE_KNL_L 侧面左膝角度均值 0.960 0.267 2.955 AVE_KNR_RA 侧面右膝角加速度均值 0.130 0.219 1.547 AVE_TR_R 侧面躯干角度均值 −1.502 −0.395 2.487 SD_SHR_R 侧面右肩角度标准差 0.049 0.137 2.386 模型 3 0.628 0.158 常数 — 0.051 — — AVE_SHL_LV 侧面左肩角速度均值 0.079 0.211 1.114 AVE_HIPL_LV 侧面左髋角速度均值 0.090 0.191 3.413 AVE_KNR_RA 侧面右膝角加速度均值 0.195 0.326 3.168 AVE_TR_RV 侧面躯干角速度均值 0.158 0.314 5.500 AVE_YA 身体中心纵向运动加速度均值 −0.291 −0.665 7.193 SD_KNR_R 侧面右膝角度标准差 −0.122 −0.249 2.599 SD_YV 身体中心纵向运动速度标准差 0.362 0.893 6.111 注：β1表示非标准化系数，β2表示标准化系数。
下载: 导出CSV
表 8 模型测量误差结果
Table 8 Error results of models
误差指标 模型1 模型1-1 模型2 模型2-1 模型3 模型3-1 MAE/METs 0.96 0.84 0.89 0.76 0.81 0.74 MSE/METs 1.53 1.16 1.36 1.00 1.11 0.91 RMSE/METs 1.19 0.97 1.14 0.96 1.02 0.92 MRE/% 17.14 14.80 15.13 12.90 13.60 12.33 注：模型1基于正面运动指标建立，模型2基于侧面运动指标建立，模型3基于正面和侧面运动指标建立，模型1-1、模型2-1和模型3-1分别在模型1、2、3的基础上加入了%HRR。
下载: 导出CSV
-
[1] 林英禄.运动数据的实时监测与健康评价模型的研究[D].上海: 华东师范大学, 2015: 1-2 [2] 邱淑敏,王欢,江崇民.运动健身能量消耗简易测量方法的效度研究[J]. 体育科学,2013,33(6):69-76 doi: 10.3969/j.issn.1000-677X.2013.06.010 [3] 王欢,王馨塘,佟海青,等.三种加速度计测量多种身体活动的效度比较[J]. 体育科学,2014,34(5):45-50,65 doi: 10.3969/j.issn.1000-677X.2014.05.007 [4] 朱琳,陈佩杰.能量消耗测量方法及其应用[J]. 中国运动医学杂志,2011,30(6):577-582 doi: 10.16038/j.1000-6710.2011.06.002 [5] 段峰,王耀南,雷晓峰,等.机器视觉技术及其应用综述[J]. 自动化博览,2002,19(3):59-61 doi: 10.3969/j.issn.1003-0492.2002.03.020 [6] GRAY A,ANDREWS M,WALDRON M,et al. A model for calculating the mechanical demands of overground running[J]. Sports Biomechanics,2020:1-22
[7] ZHANG J C,LIU S Q,ZHU R. Motion velocity,acceleration and energy expenditure estimation using micro flow sensor[J]. IEEE Access,2019,7:75901-75909 doi: 10.1109/ACCESS.2019.2921978
[8] LIN B S,WANG L Y,HWANG Y T,et al. Depth-camera-based system for estimating energy expenditure of physical activities in gyms[J]. IEEE Journal of Biomedical and Health Informatics,2019,23(3):1086-1095 doi: 10.1109/JBHI.2018.2840834
[9] NATHAN D,HUYNH D Q,RUBENSON J,et al. Estimating physical activity energy expenditure with the Kinect Sensor in an exergaming environment[J]. PLoS One,2015,10(5):e0127113 doi: 10.1371/journal.pone.0127113
[10] CARLSON J A,LIU B O,SALLIS J F,et al. Automated high-frequency observations of physical activity using computer vision[J]. Medicine and Science in Sports and Exercise,2020,52(9):2029-2036 doi: 10.1249/MSS.0000000000002341
[11] CAO Z,HIDALGO G,SIMON T,et al. OpenPose:Realtime multi-person 2D pose estimation using part affinity fields[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2021,43(1):172-186 doi: 10.1109/TPAMI.2019.2929257
[12] 田冬.基于深度学习的骨架序列−视频动作识别研究[D].杭州: 浙江大学, 2020: 22-32 [13] 黎涌明.摄氧量动力学:历史、特征和启示[J]. 武汉体育学院学报,2015,49(3):63-69 doi: 10.3969/j.issn.1000-520X.2015.03.011 [14] CUST E E,SWEETING A J,BALL K,et al. Machine and deep learning for sport-specific movement recognition:A systematic review of model development and performance[J]. Journal of Sports Sciences,2019,37(5):568-600 doi: 10.1080/02640414.2018.1521769
[15] CAO Z B,MIYATAKE N,HIGUCHI M,et al. Predicting VO2max with an objectively measured physical activity in Japanese men[J]. European Journal of Applied Physiology,2010,109(3):465-72 doi: 10.1007/s00421-010-1376-z
[16] GUESS T M,RAZU S,JAHANDAR A,et al. Comparison of 3D joint angles measured with the Kinect 2.0 skeletal tracker versus a marker-based motion capture system[J]. Journal of Applied Biomechanics,2017,33(2):176-181 doi: 10.1123/jab.2016-0107
[17] MOORE C C,AGUIAR E J,DUCHARME S W,et al. Development of a cadence-based metabolic equation for walking[J]. Medicine and Science in Sports and Exercise,2021,53(1):165-173 doi: 10.1249/MSS.0000000000002430
[18] LI M N,KWAK K C,KIM Y T. Intelligent predictor of energy expenditure with the use of patch-type sensor module[J]. Sensors,2012,12(11):14382-14396 doi: 10.3390/s121114382
[19] ALTINI M,PENDERS J,VULLERS R,et al. Estimating energy expenditure using body-worn accelerometers:A comparison of methods,sensors number and positioning[J]. IEEE Journal of Biomedical and Health Informatics,2015,19(1):219-226 doi: 10.1109/JBHI.2014.2313039
[20] 李海燕,陈佩杰,庄洁.11~16岁肥胖青少年体力活动耗氧量推算方法实验研究[J]. 中国运动医学杂志,2010,29(2):217-220 doi: 10.16038/j.1000-6710.2010.02.008 [21] FREEDSON P S,MELANSON E,SIRARD J. Calibration of the computer science and applications, Inc. accelerometer[J]. Medicine and Science in Sports and Exercise,1998,30(5):777-781 doi: 10.1097/00005768-199805000-00021
[22] HAWKINS D,MOLÉ P. Modeling energy expenditure associated with isometric,concentric,and eccentric muscle action at the knee[J]. Annals of Biomedical Engineering,1997,25(5):822-830 doi: 10.1007/BF02684166
[23] VILLARS C,BERGOUIGNAN A,DUGAS J,et al. Validity of combining heart rate and uniaxial acceleration to measure free-living physical activity energy expenditure in young men[J]. Journal of Applied Physiology,2012,113(11):1763-1771
[24] GASTIN P B,CAYZER C,DWYER D,et al. Validity of the ActiGraph GT3X+ and BodyMedia SenseWear Armband to estimate energy expenditure during physical activity and sport[J]. Journal of Science and Medicine in Sport,2018,21(3):291-295 doi: 10.1016/j.jsams.2017.07.022
[25] 汤强,盛蕾,朱卫红.体力活动研究中加速度计的应用[J]. 体育科学,2009,29(1):77-84,91 doi: 10.3969/j.issn.1000-677X.2009.01.011 [26] BI Z,HUANG W J. Human action identification by a quality-guided fusion of multi-model feature[J]. Future Generation Computer Systems,2021,116:13-21 doi: 10.1016/j.future.2020.10.011
[27] JACK H, DAVID L, COSTILL W, 等.运动生理学[M]. 4版. 王瑞元, 汪军, 译. 北京: 北京体育大学出版社, 2008: 42 [28] 严波涛,许建辉.人体机械功计算方法的实验研究[J]. 西安体育学院学报,1993,10(1):27-34,81 doi: 10.16063/j.cnki.issn1001-747x.1993.01.008 [29] 柏树令, 应大君.系统解剖学[M].北京: 人民卫生出版社, 2005: 90 [30] KERN D S,SEMMLER J G,ENOKA R M. Long-term activity in upper- and lower-limb muscles of humans[J]. Journal of Applied Physiology,2001,91(5):2224-2232 doi: 10.1152/jappl.2001.91.5.2224
[31] 朱卫红.上肢活动加速度与能量消耗特征初探[D]. 苏州: 苏州大学, 2009: 33-38 [32] CHAFFIN D B.The development of a prediction model for the metabolic energy expended during arm activities[D]. State of Michigan: The University of Mechigan, 2006: 202-212
[33] JORDAN M,DONNE B,FLETCHER D. Only lower limb controlled interactive computer gaming enables an effective increase in energy expenditure[J]. European Journal of Applied Physiology,2011,111(7):1465-1472 doi: 10.1007/s00421-010-1773-3
[34] WILLEMS P A,CAVAGNA G A,HEGLUND N C. External,internal and total work in human locomotion[J]. The Journal of Experimental Biology,1995,198(Pt 2):379-393
[35] KARANTONIS D M,NARAYANAN M R,MATHIE M,et al. Implementation of a real-time human movement classifier using a triaxial accelerometer for ambulatory monitoring[J]. IEEE Trans Inf Technol Biomed,2006,10(1):156-167 doi: 10.1109/TITB.2005.856864
[36] HEYWARD V H. Advanced fitness assessment and exercise prescription[J]. Medicine and Science in Sports and Exercise,1992,24(2):278
[37] HASKELL W L,LEE I M,PATE R R,et al. Physical activity and public health:Updated recommendation for adults from the American College of Sports Medicine and the American Heart Association[J]. Medicine and Science in Sports and Exercise,2007,39(8):1423-1434 doi: 10.1249/mss.0b013e3180616b27
[38] CHANG C H,LIN K C,HO C S,et al. Accuracy of the energy expenditure during uphill exercise measured by the Waist-worn ActiGraph[J]. Journal of Exercise Science & Fitness,2019,17(2):62-66
[39] WELTMAN A,WELTMAN J,RUTT R,et al. Percentages of maximal heart rate,heart rate reserve,and V̇O2peak for determining endurance training intensity in sedentary women[J]. International Journal of Sports Medicine,1989,10(3):212-216 doi: 10.1055/s-2007-1024903
[40] RIEBE D, EHRMAN J, LIGUORI G, et al. ACSM's guidelines for exercise testing and prescription[M]. 10th ed. Philadelphia: Wolters Kluwer, 2018: 2-5
[41] NORMAN J F,HOPKINS E,CRAPO E. Validity of the counting talk test in comparison with standard methods of estimating exercise intensity in young healthy adults[J]. Journal of Cardiopulmonary Rehabilitation and Prevention,2008,28(3):199-202 doi: 10.1097/01.HCR.0000320072.89093.0d
[42] CUI Y P,LIU X Y,LIU X R,et al. Evaluation of the exercise workload of broadcast calisthenics for children and adolescents aged 11-17 years[J]. Journal of Sports Sciences,2011,29(4):363-371 doi: 10.1080/02640414.2010.533688
-
期刊类型引用(4)
1. 张萱，干静. 基于OpenPose动作姿态分析的健身器材可用性研究. 机电产品开发与创新. 2025(01): 21-25 . 
百度学术
2. 丁海峰，刘韵婷，张兴伟，王嘉烨. 基于改进OpenPose的引体向上检测算法研究. 通信与信息技术. 2025(01): 51-54 . 百度学术
3. 曹璐华. 基于EVM测量算法的移动终端接入控制技术. 吉林大学学报(信息科学版). 2024(05): 966-971 . 百度学术
4. 王轶凡，温煦. 从直接测热法到计算机视觉技术：身体活动能量消耗测量的历史与未来. 上海体育学院学报. 2023(04): 92-104 . 百度学术
其他类型引用(5)
计量
- 文章访问数: 512
- HTML全文浏览量: 374
- PDF下载量: 65
- 被引次数: 9