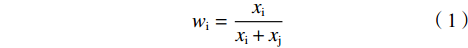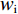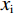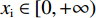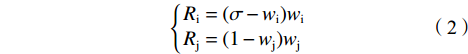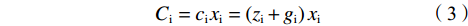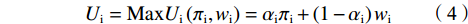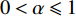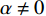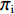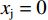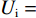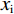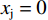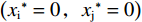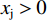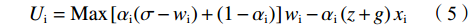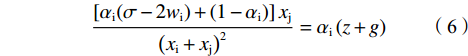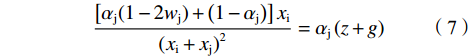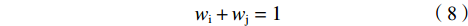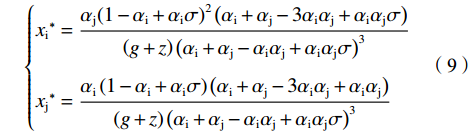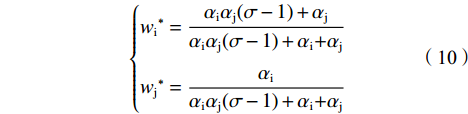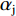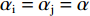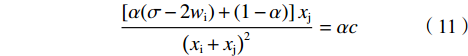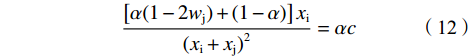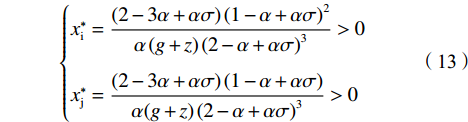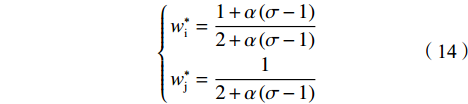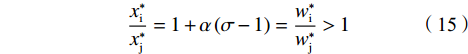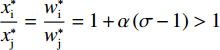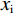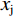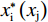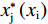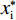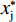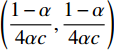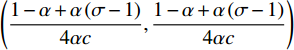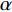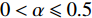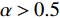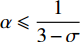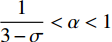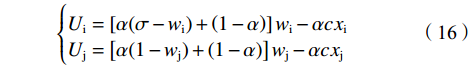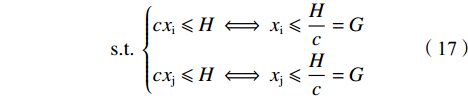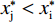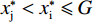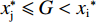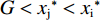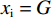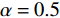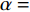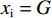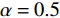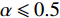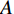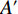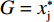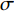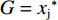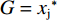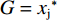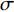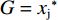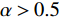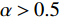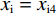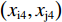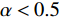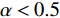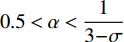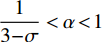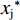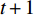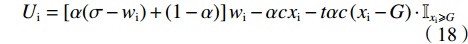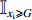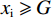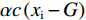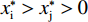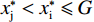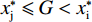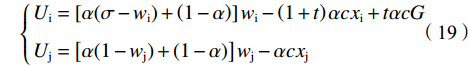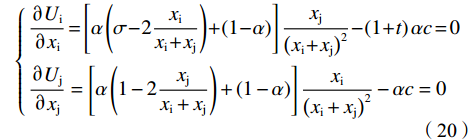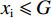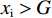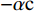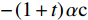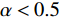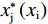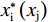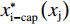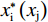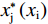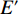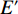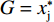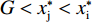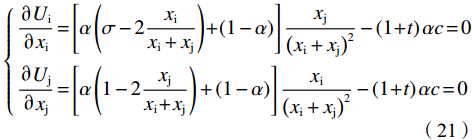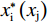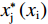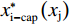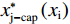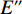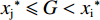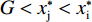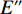Salary Cap Policy in Professional Sports Leagues: System Evolution, Mechanism and Policy Implications
-
摘要:
工资帽政策作为防止“金元体育”无序扩张、控制俱乐部运行成本、促进联盟竞争性平衡的规制工具，近年来已逐渐应用于中国职业体育联盟。比较分析工资帽政策在国内外主要联赛中的制度演进与分化历程，并通过博弈论与静态优化方法分析不同类型工资帽政策的适用条件及其对俱乐部最优投资和竞争性平衡的影响，发现：①俱乐部的均衡投资与利润权重呈负相关，与俱乐部禀赋（盈利能力）差异呈正相关，而竞争性平衡与利润权重、俱乐部禀赋差异都呈负相关；②无论俱乐部更看重胜率还是利润，硬工资帽都能降低大城市俱乐部（盈利能力强）的投资、促进竞争性平衡，但对小城市俱乐部（盈利能力差）投资的作用不太明确；③软工资帽只有在不太严格的临界值下才能促进竞争与限制投资，但效果总是次于硬工资帽政策。提出政策建议：①完善硬工资帽政策的制定与实施，对于软工资帽政策则需审慎选择；②推进俱乐部股权多元化结构性改革，合理控制胜率最大化和利润最大化股东比例；③有效把控工资帽政策规制力度，主动应对新冠病毒感染疫情冲击下的球员欠薪、球队破产等问题。
Abstract:As a powerful tool for preventing the disorderly expansion of "sugar daddy's game", controlling the operating costs of clubs, and promoting competitive balance in leagues, the salary cap policy has gradually been applied to China's professional sports leagues in recent years. This paper first provides comparative analysis of the institutional evolution and differentiation of salary cap policies in major domestic and international leagues. We then focus on analyzing the conditions under which the two types of hard and soft salary caps are applied and their impact on the optimal investment and competitive balance of clubs with different target orientations, using both game-theoretic and static optimization methods. The findings indicate that: ① The equilibrium investment of clubs is negatively correlated with the weight of profits and positively correlated with the difference in club endowments (profitability). However, the competitive balance is negatively correlated with both the profit weighting and the difference in club profitability. ② Regardless of whether a club values winning or profit, a hard salary cap can reduce investment by clubs with strong profitability in large city markets and promote competitive balance. However, its impact on investment by clubs in small city markets, where profitability is poor, is less clear. ③ A soft salary cap can only promote competition and limit investment at a less strict critical value, but its effectiveness is inferior to that of a hard salary cap policy. Based on the above, the following suggestions are proposed: ① Further improve the formulation and implementation of hard salary cap policies and make them the main regulatory scheme, while selecting soft salary cap policies carefully; ② Promote structural reform of club equity diversification, reasonably control the proportion of shareholders seeking to maximize win rate and profit, and seek a balance between restricting excessive investment and promoting league recovery; ③ Reasonably control the strength of salary cap policy regulation and proactively respond to issues such as player arrears and team bankruptcies under the impact of the COVID-19 pandemic.
-
Keywords:
- contest theory /
- salary cap /
- luxury tax /
- investment strategy /
- competitive balance
-
在当前国内外体育经济学研究与职业体育联盟实际操作过程中，工资帽已越来越成为交叉补贴政策[1-3]中应用与讨论最为广泛的规制政策。常见的工资帽政策有2种：一种是美国国家橄榄球联盟（NFL）、北美职业冰球联盟（NHL）与中国职业足球超级联赛（CSL）等采用的硬工资帽政策，即严格禁止俱乐部工资支出超过某一界线；另一种是以美国职业篮球联盟（NBA）与中国职业篮球联赛（CBA）为代表的软工资帽政策，即当工资超过工资帽临界值后，俱乐部须缴纳一定比例的罚款。关于工资帽政策的作用机制与规制效果，国内外学术界展开了一系列研究[3-9]，但目前还没有一个统一的框架对不同类型工资帽政策的异同进行梳理，也没有一种通用框架可完整剖析工资帽政策中各类规制手段对俱乐部投资与联盟竞争性平衡的作用机制。
（1）竞赛理论在职业体育联盟中的应用。职业体育联盟中的俱乐部竞争是一种处于“战略联盟”约束下的特殊寡头市场。在这种战略联盟中，俱乐部通过合作与竞争共同生产比赛，同时，赢取冠军能为俱乐部带来更多奖励与注意力相关收益。因此，俱乐部不仅关注竞赛过程中产生的成本与收益，还关注能否在联盟中获得领先地位或最终的冠军。事实上，这种争夺冠军的博弈过程早在20世纪80年代就被Tullock[10]、Lazear等[11]、Konrad[12]发展为“竞赛理论”，并广泛应用于公共资源分配的寻租、官员晋升锦标赛、专利与研发竞赛以及体育竞赛等领域。此后，在竞赛理论的基本理论框架下，Baik[13]、Chung[14]、Dixit[15]、Fu等[16]、Gelder等[17]对竞赛中参赛者的策略性努力与过度投资等行为进行了一系列讨论。在体育领域，Szymanski[18]首次将竞赛理论应用于职业体育联盟，而后瑞士苏黎世大学的学者们做出进一步拓展，如：Grossmann等[19]基于竞赛理论提出俱乐部人才投资的两阶段模型，基于一个严格凸的成本函数证明了竞赛中存在多重均衡；Dietl等[20-21]提出体育竞赛领域的过度投资问题，认为参赛者异质性会驱动俱乐部做出不同投资决策，而这些决策差异是造成俱乐部过度投资的本质原因。Leach等[22]在竞赛模型中考虑了俱乐部目标函数差异对其均衡投资和联盟竞争性平衡的影响，并通过实证数据证明了欧洲足球俱乐部是胜率最大化而非利润最大化。本文遵循竞赛理论及其应用在职业体育联盟中的基本框架，同时嵌入不同俱乐部在胜率最大化或利润最大化上的显著差异，并考虑俱乐部将胜率转化为利润时的异质性，讨论在这种一般性的竞赛模型中工资帽政策在限制投资和促进竞争方面的效果。
（2）工资帽政策对竞赛参与人的努力与联盟竞争性平衡的影响。在主流经济学文献中，关于竞赛中的工资帽政策可追溯至Che等[23-24]关于政治选举竞赛中募捐上限问题的研究，他们将政治选举竞争描述为2个参与人的完全、非对称信息下的全付费拍卖（All Pay Auction），发现对竞选捐款设置严格上限（Rigid Bid Caps）会在增加总捐款的同时降低参赛者总盈余。Gavious等[25]、Sahuguet[26]在2个参与人的不完全、非对称信息下的全付费拍卖中考虑了刚性出价上限，发现Che等[23]的结果在凸成本时也可扩展至不完全信息。Kaplan等[27]则反驳了Che等[23]的观点，认为将严格的募捐上限放松为更灵活的形式（Flexible Bid Cap），支出上限确实可以减少总支出。此后，Olszewski等[28]和Fu等[29]又分别在多个参与人的全付费拍卖与塔洛克彩票竞赛（Tullock Lottery Contest）中比较了刚性上限与灵活上限对支出与税收的影响，发现无论设计者偏好如何，刚性出价上限总是被柔性出价上限超越；但当设计者只关注总出价时，无上限的自由放任政策是最优的。具体到职业体育联盟，Szymanski[18]首次将竞赛理论应用于职业体育，并建模分析了竞赛结构中交叉补贴制度对俱乐部投资与联盟竞争性平衡的影响，发现收益共享机制首先会降低所有俱乐部的投资与努力，但弱队在共享机制下从强队得到的收益比强队在共享机制下从弱队得到的收益更多，因此弱队更有动机去降低投资，从而使得联盟竞争性平衡降低；同时，当俱乐部追求胜率最大化时，工资帽与奢侈税等政策的效果与收益共享完全一致。次年，Szymanski等[30]再次阐述上述观点，并引入标准的产业组织模型进行证明。Peeters等[31]则首次使用结构模型对工资帽政策效果进行模拟，发现工资帽政策对竞争性平衡的促进效果比财务公平竞争法案更好。本文职业体育联盟中的硬工资帽、软工资帽政策与塔洛克彩票竞赛中刚性出价上限、灵活出价上限的特征异曲同工，但进一步考虑了职业体育联赛的“生产过程”。相较于Szymanski[18]的研究只考虑利润最大化假设下工资帽与奢侈税对均衡投资的影响，本文综合考虑利润/获胜最大化2种目标函数，并讨论了不同权重对竞赛结果的影响；相较于Peeters等[31]的研究，本文则在理论模型上进行了进一步拓展。
（3）涉及工资帽与奢侈税的其他体育经济学理论与实证研究。①工资帽。大部分文献都认为工资帽能够限制自由市场上的球员向大俱乐部集中，有助于提高竞争性平衡。如在理论模型中，Fort等[3]对比了各种交叉补贴政策，认为工资帽是当时所使用的交叉补贴政策中唯一可以提高联赛竞争性平衡目标的方案；Kesenne[6]、Dietl等[21]认为工资帽政策提高了联盟竞争性平衡，改善了球员工资分配，抑制了顶级球员过高的工资支出，保证了俱乐部合理的利润率。在实证研究中，Booth[4]通过对澳大利亚足球（AFL）、橄榄球（NRL）与篮球（NBL）联盟的研究发现，引进工资帽能够改善竞争性平衡，但同时也可能受到俱乐部数量和俱乐部所在城市变化的影响。Larsen等[8]发现，在NFL联赛中引入工资帽政策也能够增加竞争性平衡。Chatzistamoulou等[5]采用两阶段方法评估NBA俱乐部绩效时发现，引入工资帽政策缩小了俱乐部间的效率差异，有利于促进平衡。同时也存在许多反对观点，如：Rottenberg[32]提出了不变性命题（Invariance Proposition），认为只要产权是确定的，那么竞争性平衡就不会受到制度变化的影响；Vrooman[9]研究发现，在利润最大化联盟中工资帽使俱乐部之间形成的联盟像卡特尔（cartel）中的公司一样相互勾结，导致俱乐部对球员的更多剥削和竞争性平衡的降低；Kesenne[7]通过实证研究也发现，在欧洲足球G-14（2000—2008年由14家欧洲豪门俱乐部组成的联盟）中引入工资帽会对人才分配和联赛竞争性平衡产生负面影响。②奢侈税。Gustafson等[33]、Marburger[34]最早建模分析了封闭式联盟中奢侈税对球员薪资和竞争性平衡的影响，并发现奢侈税会提高竞争性平衡，同时有效减少球员工资支出。此后，Gustafson[35]、Dietl等[36]进一步证明了奢侈税对竞争性平衡的正向影响。Maxcy[37]对美国职业棒球大联盟（MLB）的研究发现，奢侈税政策不能有效抑制高收入俱乐部的支出，因此为了更公平地分配人才，MLB有必要模仿NFL和NHL设置硬性工资上限。
无论是硬工资帽还是奢侈税，其效果在理论与实践中都不存在完全肯定的答案。究其原因，主要在于不同模型设置存在较大差异，如俱乐部目标函数差异、俱乐部禀赋差异等。相较于以上文献，本文的边际贡献在于，严格遵循竞赛理论的基本框架，假设球员边际成本不变且对于不同俱乐部其值相同，同时考虑俱乐部在目标函数上遵循胜率最大化或利润最大化的显著差异，试图以一个一般性框架对不同类型的工资帽政策的效果做进一步分析。本文比较分析了工资帽政策在国内外主要联赛中的制度演进与分化过程；基于竞赛理论构建了俱乐部投资竞争的理论模型，对2种工资帽约束下的最优问题进行求解，并比较分析了2种规制政策的适用条件及效果差异；基于制度演进与数理分析提出对中国职业体育联赛的建议。本文从竞赛理论出发，利用博弈论与静态优化方法构建一个完整的框架，重点对俱乐部层次的硬工资帽与软工资帽政策效果进行系统研究，以期为CSL、CBA工资帽政策实践提供指导。
1. 工资帽政策的制度演进
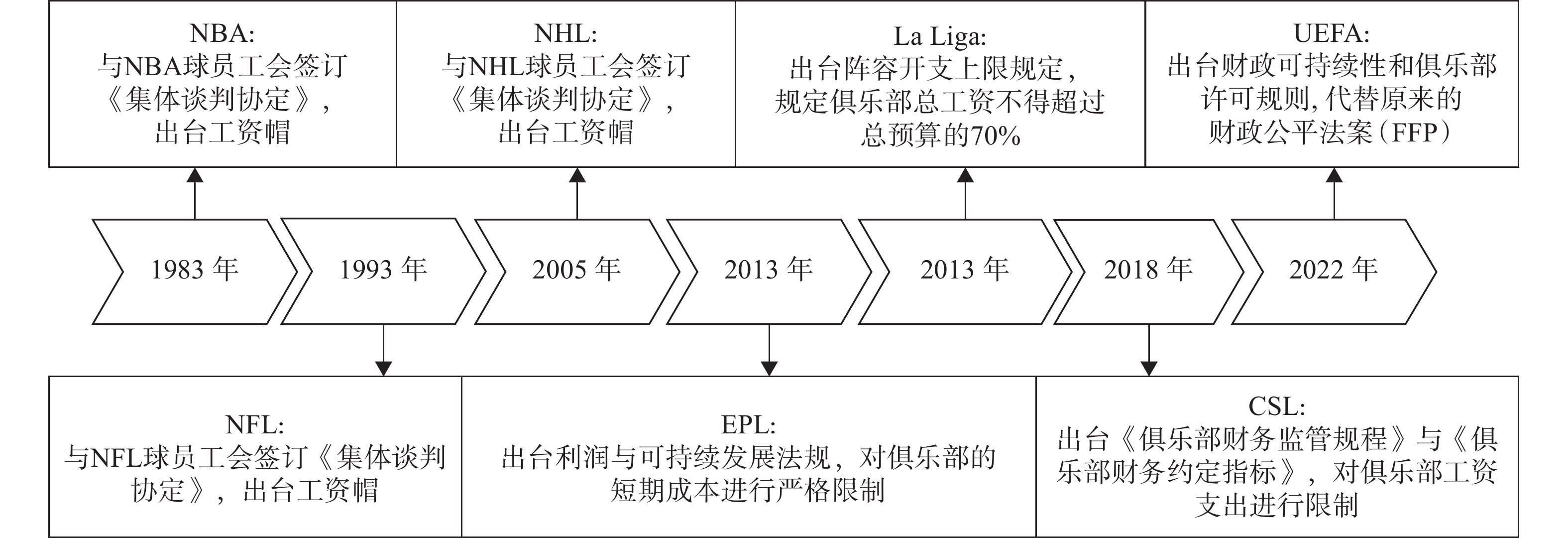
工资帽政策，简单来说就是联盟（协会）规定俱乐部工资支出禁止超过某一界线，其自1984年引入NBA后就迅速在不同职业体育联赛中扩张。不同联赛在具体制度选择上有各自的实践：有的采用硬工资帽政策，有的采用软工资帽政策；有的采用工资上限，有的设置工资下限；有的针对俱乐部总体，有的针对球员个体；有的基于俱乐部过去收入，有的基于预算支出。总体而言，其中最主要的差异还是到底采用硬工资帽还是软工资帽政策？这2种方式在政策制定与实施效果上存在较大差别。针对这一分歧，下文主要以软、硬工资帽政策为分类标准，对比分析工资帽政策的演进历程及其分化逻辑。
1.1 硬工资帽政策的制度演进
硬工资帽政策源于1983年NBA与其球员工会签订的集体谈判协定（Collective Bargaining Agreement，即劳资协定）。该协定规定，联盟中各俱乐部的工资支出不得超过联盟上赛季篮球相关收入（Basketball-Related Income，BRI）的一个固定比例（最初为53%）除以俱乐部数量，同时也不得低于工资上限的75%。随后在1993年，NFL与其球员工会达成的劳资协定也规定，俱乐部总支出不得超过联盟预算总收入的58%除以俱乐部数量再减去福利资金。与NBA工资帽不同，NFL的工资帽政策遵从“以收定支”的监管思想，即根据俱乐部预算决定俱乐部工资支出，而非像NBA根据联盟上赛季收入决定下赛季工资帽限额。2005年，NHL与其球员工会签订的劳资协定也设置了基于联盟收入的硬性工资上限（前一赛季联盟总收益的某一固定比例，最初为75%）与工资下限（最初为55%）。总体而言，20世纪80年代至21世纪初，工资帽政策主要在北美职业体育联盟中流行，所涉及的也都是封闭式联盟，俱乐部往往追求利润最大化而非胜率最大化。同时，工资帽限额的确定也都是基于收入或预算的某一比例计算，并非直接固定某一个数值，而是需要根据每年的收支进行调整。
2013年，英国足球超级联赛（EPL）出台了俱乐部利润与可持续发展法规（Profit and Sustainability Regulations，PSR），对俱乐部的短期成本进行了严格限制（Short-Term Cost Control，STCC），这也是硬工资帽首次应用于欧洲职业足球联赛。PSR规定，自2014赛季起，任何年薪总支出超过5200万英镑的俱乐部在未来3年内只允许提薪400万英镑（其中商业收入和比赛分成不计算在内），否则将被处以联赛扣分的严厉惩罚。同年，西班牙足球甲级联赛（La Liga，以下简称“西甲”）也出台了阵容开支上限规定（Squad Cost Limit，SCL），规定俱乐部总工资不得超过俱乐部总预算的70%。可以发现，西甲工资帽与NFL的工资帽类似，其核心监管思想也是“以收定支”，即根据预算决定俱乐部的支出上限。在中国，2018年12月中国足协出台了《中国足球协会职业足球俱乐部财务监管规程》和《中超俱乐部财务约定指标（2019—2021）》，规定中超俱乐部一线队薪酬总额占总支出的比例在2019—2021年分别不得超过65%、60%、55%，且任何总薪酬超过限额的俱乐部将会被处以扣分的惩罚，同时超过个人工资帽的球员不得参加中国足协管辖的各项足球赛事。2022年4月，欧足联（UEFA）最新出台的《俱乐部财政可持续性和俱乐部许可规则》将西甲的阵容成本控制规则在全欧盟进行了全面推广，规定所有参加欧足联旗下比赛的俱乐部总工资不得超过俱乐部总预算的70%。由此可见，近10年来硬工资帽政策在北美以外的职业体育市场上得到了广泛的应用，且规制方式从原来单纯地按比例计算发展为由规制机构（联盟或协会）直接制定，具体表现形式也更加多样。硬工资帽政策的发展与演进历程如图1所示。
![]()
图 1 职业体育联盟中硬工资帽政策的演进历程Figure 1. The history of hard salary cap policies in professional sports leagues1.2 软工资帽政策的制度演进
软工资帽政策始于1994—1995赛季的MLB，是一种以竞争性平衡税（Competitive Balance Tax，CBT）为表现形式的奢侈税政策。MLB劳资协定（2017版）第23条规定：2017—2021年CBT基本起征点分别为1.95亿美元、1.97亿美元、2.06亿美元、2.08亿美元、2.1亿美元。任何工资高于起征点的俱乐部，如果上一个合同年度未超过基本税起征点（即第一次缴纳CBT）则税率为20%，如果是第2次超过基准线则税率增加为30%，如果是第3次超过基准线则税率为50%。此外，MLB还存在2个附加费阈值，第1个在5年间分别为2.15亿美元、2.17亿美元、2.26亿美元、2.28亿美元、2.30亿美元；第2个为2.35亿美元、2.37亿美元、2.46亿美元、2.48亿美元，2.50亿美元。总工资支出处于2个阈值之间的部分需要加征12%的附加税，超过第2个阈值部分则需加征45%的附加税。
1999年，NBA也设立了奢侈税制度，规定联盟各俱乐部的工资支出总额若超过奢侈税阈值（Luxury Tax Threshold=BRI×55%/俱乐部数量）需要缴纳相应的罚款。具体而言，以2011年版劳资协定为例，其规定自2012年起NBA将引入阶梯形式的奢侈税计算方法，根据划档来设定奢侈税具体缴纳比例：在0~499.9万美元区间按1.5倍的税率缴纳；500万~999.9万美元区间按1.75倍的税率缴纳；1000万~1499.9万美元区间按2.5倍的税率缴纳；1500万~1999.9万美元区间按3.25倍的税率缴纳；超过2000万美元的按3.75倍的税率缴纳，且每超过500万美元税率递增0.5倍。相较于NBA在1984年引进的硬工资帽，奢侈税制度的设立体现了NBA对于工资帽实施的显著变化。究其原因，主要是一开始的硬工资帽政策存在许多漏洞，如拉里伯德条款、中层工资特例、伤病球员特例等，且未设定超过工资帽时的具体惩罚机制，因此实施效果并不好。为此，NBA联盟又进一步增加了惩罚机制，并选用了奢侈税这种“累进税”的惩罚方式。类似地，中国篮协2019年10月俱乐部投资人会议暨股东会第七次会议通过了《CBA联盟“敢梦敢当”联合宣言》，参考NBA的做法对国内球员工资进行规定：自2020—2021赛季起，工资帽基准值为3600万元，缓冲值为1200万元。实际合同工资超出工资帽上限或者低于工资帽下限的，应向联盟缴纳青训调节费。无论MLB、NBA还是CBA的工资帽政策，都是一种具有“累进税”特征的软工资帽，即只要俱乐部愿意缴纳奢侈税就可以增加大牌球员的交易。相较于NFL、NHL、CSL等联盟的硬工资帽政策，在软工资帽政策约束下俱乐部的财务控制与投资决策无疑会更加灵活，这可能也是软工资帽政策能够存在的主要原因。
1.3 国内外软、硬工资帽政策的比较
自1984年NBA首次采用后，工资帽政策已迅速扩展到其他众多职业体育联赛。在具体实施过程中，不同联赛的操作虽然有所不同（表1），但最主要的区别还是在于到底该采取硬工资帽还是软工资帽政策。其中，发源并发展于北美职业体育联盟的硬工资帽政策，近10年来已广泛运用于北美以外的职业足球联赛，这一趋势表明硬工资帽不仅在封闭式联盟中有效，在开放式联盟中也可能适用。同时，硬工资帽政策不仅在篮球运动联盟中存在，在冰球、棒球、足球运动联盟中也广泛应用，极大地证明了其适用性与可能的约束力。软工资帽政策自1994年第1次出现于MLB后，就只有NBA和CBA采用，说明其在运动项目中的普及率较低。此外，选择软工资帽政策的职业体育联盟都是封闭式联盟，而选择硬工资帽政策的联盟不仅有封闭式也有开放式，这可能也与软工资帽政策规制效果的局限性等息息相关。
表 1 国内外不同联赛工资帽政策选择与实施情况对比Table 1. Comparison of salary cap policies and implementation in different leagues联盟 俱乐部层次 球员层次 工资上限 工资下限 奢侈税 硬工资帽 NBA YES YES YES YES NFL YES NO NO NO MLB YES NO YES NO NHL YES YES NO NO EPL YES NO NO NO La Liga YES NO NO NO CSL YES NO NO YES CBA YES YES YES YES 注：只有工资上下限而没有奢侈税是硬工资帽政策，既有工资上下限又有奢侈税是软工资帽政策。 事实上，对于上述问题，Fort等[3]关于不同交叉补贴政策规制效果的研究发现：硬工资帽政策相对于其他职业体育联盟的交叉补贴政策而言是最优的。Maxcy[37]对MLB的研究也发现，奢侈税政策远比硬工资帽政策的规制效果差。在最近的研究中，如Fu等[29]在比较刚性上限与灵活上限对支出与税收的影响时发现，无论设计者的偏好如何，刚性出价（硬工资帽政策）总是被柔性出价（软工资帽政策）超越。可见，2种工资帽政策的效果其实还并不清晰。本文沿用职业体育经济学中广泛使用的竞赛理论，将影响俱乐部投资决策的俱乐部目标函数差异、俱乐部盈利能力差异、俱乐部成本函数差异等纳入统一的研究框架，讨论2个参与人竞赛中针对俱乐部总体的硬工资上限与奢侈税这2种政策的效果与其适用条件，以期为“后疫情”时期中超、CBA以及英雄联盟职业联赛（LPL）等为了控制俱乐部运营成本、维持联盟稳定而引进与改革的工资帽、奢侈税以及与工资帽类似的引援调节费等政策提供理论依据与实践方向。
2. 工资帽政策的作用机理
2.1 模型设定与无约束均衡
2.1.1 基本假设
假设1：假设在由2个俱乐部i、j组成的职业体育联盟中，俱乐部为获胜而竞争。在这一竞争过程中，俱乐部间相互博弈，不存在联盟与俱乐部的博弈，因此可将联盟规制视为外生变量。其中，俱乐部胜率遵循由Tullock[10]、Lazear等[11]、Dixit[15]、Rosen[38]、Skaperdas[39]提出，Szymanski[18]、Leach等[22]、Dietl等[40]应用于体育经济学建模的竞赛成功函数（Contest Success Function，CSF）：
$$ {w}_{\rm{i}}=\frac{{x}_{\rm{i}}}{{x}_{\rm{i}}+{x}_{\rm{j}}} $$ (1) 其中：
${w}_{\rm{i}}$ 表示俱乐部i在竞赛中获胜的概率；$ {x}_{\rm{i}} $ 表示俱乐部i中球员才能的总量（Total Talent），且$ {x}_{\rm{i}}\in [0,+\infty ) $ 。假设2：沿用Leach等[22]的基本设定，假设俱乐部收益函数是关于胜率的凹函数，且不同俱乐部获胜带来的收入非对称，将俱乐部收益函数设为：
$$\left\{ \begin{gathered} {R_{\text{i}}} = (\sigma - {w_{\text{i}}}){w_{\text{i}}} \\ {R_{\text{j}}} = (1 - {w_{\text{j}}}){w_{\text{j}}} \\ \end{gathered} \right. $$ (2) 其中，
$ \sigma $ 是俱乐部i的盈利能力相较俱乐部j的倍数。假设俱乐部j盈利能力较差，那么$ \sigma \geqslant 1 $ 。具体而言，如果2个俱乐部所在城市市场规模不同，那么其观众的规模也不同，此时同样赢得一场比赛时大城市俱乐部能够获得的收益预期会比小城市俱乐部更高[9]。为方便解释，统一假定：俱乐部i为大城市俱乐部，其盈利能力较强；俱乐部j为小城市俱乐部，其盈利能力较差。假设3：假设俱乐部持有球员的成本是线性的，其边际成本为常数c（且
$ c > 0 $ ）[41]，而固定成本标准化为0，俱乐部的成本函数可表示为：$$ {C}_{\rm{i}}={c}_{\rm{i}}{x}_{\rm{i}}=\left({z}_{\rm{i}}+{g}_{\rm{i}}\right){x}_{\rm{i}} $$ (3) 其中，z表示每单位球员才能（Per Talent）所需要支付的转会费，g表示每单位球员才能所需要支付的工资，
$ {C}_{\rm{i}} $ 为俱乐部i的成本函数，c为球员才能的单位成本。当各俱乐部的边际成本相同时，可令$ {c}_{\rm{i}}={c}_{\rm{j}}=c $ 。假设4：体育经济学文献对俱乐部目标函数存在效用最大化假设[42-46]和利润最大化假设[47-48]。为不失一般性，本文参考Lang等[49]和Peeters等[31]的模型设定方式，认为俱乐部目标函数是两者加权：
$$ {U}_{\rm{i}}=\mathrm{M}\mathrm{a}\mathrm{x}{U}_{\rm{i}}\left({\pi }_{\rm{i}},{w}_{\rm{i}}\right)={\alpha }_{\rm{i}}{\pi }_{\rm{i}}+\left(1-{\alpha }_{\rm{i}}\right){w}_{\rm{i}} $$ (4) 其中：
$ 0 < \alpha \leqslant 1 $ 表示俱乐部对利润的重视程度；$ \alpha \ne 0 $ 是为了保证函数近似为凹函数；$ {\pi }_{\rm{i}} $ 为俱乐部i的利润，是俱乐部收益与成本函数之差。2.1.2 无约束下的均衡解
（1）当
$ {x}_{\rm{j}}=0 $ 时，根据公式（1）至（4）可知：${U}_{\rm{i}}= \left[{\alpha }_{\rm{i}}(\sigma - 1) + \left(1 - {\alpha }_{\rm{i}}\right)\right] - {\alpha }_{\rm{i}}\left(z + g\right){x}_{\rm{i}} = \left({\alpha }_{\rm{i}}\sigma - 2{\alpha }_{\rm{i}} - 1\right) - {\alpha }_{\rm{i}}\left(z + g\right){x}_{\rm{i}}$ ，且是单调减函数，因此$ {x}_{\rm{i}} $ 的最优取值为0。对于俱乐部j而言，同样$ {x}_{\rm{j}}=0 $ 为最优解。因此，$ \left({{x}_{\rm{i}}}^{*}=0，{{x}_{\rm{j}}}^{*}=0\right) $ 是一个均衡解。下文的分析暂时不考虑上述零点均衡解，而将讨论重点放在非零均衡解上。（2）当
$ {x}_{\rm{j}} > 0 $ 时，根据公式（1）至（4）可知，俱乐部的目标函数是最大化胜率和利润的加权：$$ {U}_{\rm{i}}={\rm{Max}}\left[{\alpha }_{\rm{i}}(\sigma -{w}_{\rm{i}})+\left(1-{\alpha }_{\rm{i}}\right)\right]{w}_{\rm{i}}-{\alpha }_{\rm{i}}\left(z+g\right){x}_{\rm{i}} $$ (5) 一阶条件FOC整理可得：
$$ \frac{\left[{\alpha }_{\rm{i}}(\sigma -2{w}_{\rm{i}})+\left(1-{\alpha }_{\rm{i}}\right)\right]{x}_{\rm{j}}}{{\left({x}_{\rm{i}}+{x}_{\rm{j}}\right)}^{2}}={\alpha }_{\rm{i}}\left(z+g\right) $$ (6) 由函数对称性可知，对于俱乐部j存在：
$$ \frac{\left[{\alpha }_{\rm{j}}(1-2{w}_{\rm{j}})+\left(1-{\alpha }_{\rm{j}}\right)\right]{x}_{\rm{i}}}{{({x}_{\rm{i}}+{x}_{\rm{j}})}^{2}}={\alpha }_{\rm{j}}\left(z+g\right) $$ (7) 由于假设1是基于2个俱乐部提出的，因此胜率和为：
$$ {w}_{\rm{i}}+{w}_{\rm{j}}=1 $$ (8) 联立式（6）~（8）可得：
$$ \left\{\begin{aligned} & {{x}_{\rm{i}}}^{*}=\frac{{\alpha }_{\rm{j}}{\left(1-{\alpha }_{\rm{i}}+{\alpha }_{\rm{i}}\sigma \right)}^{2}\left({\alpha }_{\rm{i}}+{\alpha }_{\rm{j}}-3{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}+{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}\sigma \right)}{\left(g+z\right){\left({\alpha }_{\rm{i}}+{\alpha }_{\rm{j}}-{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}+{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}\sigma \right)}^{3}} \\&{{x}_{\rm{j}}}^{*}=\frac{{\alpha }_{\rm{i}}\left(1-{\alpha }_{\rm{i}}+{\alpha }_{\rm{i}}\sigma \right)\left({\alpha }_{\rm{i}}+{\alpha }_{\rm{j}}-3{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}+{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}\right)}{\left(g+z\right){\left({\alpha }_{\rm{i}}+{\alpha }_{\rm{j}}-{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}+{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}\sigma \right)}^{3}} \end{aligned}\right. $$ (9) $$\left\{\begin{split} & {{w}_{\rm{i}}}^{*}=\dfrac{{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}(\sigma -1)+{\alpha }_{\rm{j}}}{{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}(\sigma -1)+{\alpha }_{\rm{i}}{+\alpha }_{\rm{j}}}\\ &{{w}_{\rm{j}}}^{*}=\dfrac{{\alpha }_{\rm{i}}}{{\alpha }_{\rm{i}}{\alpha }_{\rm{j}}(\sigma -1)+{\alpha }_{\rm{i}}{+\alpha }_{\rm{j}}} \end{split}\right. $$ (10) 分析公式（9）可知：
性质1：2个俱乐部无约束下的均衡投资均为正，但其相对大小取决于俱乐部赋予利润的权重和盈利能力的差距。①当盈利能力差距较小时，大城市俱乐部均衡投资量更大。②当盈利能力差距较大时：如果小城市俱乐部利润的权重足够大，则大城市俱乐部的均衡投资量依然更大；如果小城市俱乐部利润的权重不够大，则只有在大城市俱乐部对利润的重视程度未能远超小城市俱乐部时才会出现更大的均衡投资；如果小城市俱乐部利润的权重不够大，且大城市俱乐部对利润的重视程度远超小城市俱乐部，则大城市俱乐部的均衡投资反而比小城市俱乐部的均衡投资量要小。
性质2：俱乐部均衡投资是利润权重的负相关函数、盈利能力差异的正相关函数。
2.1.3 权重系数的简化与均衡分析
经典的竞赛理论与体育经济学相关研究均指出，俱乐部对利润与胜率重视程度的区别是异质性的重要来源，如同一联盟中不同俱乐部股权性质存在显著差异[50-54]，控股股东持有俱乐部的动机明显不同[49, 55-57]，都会造成俱乐部在追求利润最大化与胜率最大化上出现严重分歧，在模型中则表现为
$ {\alpha }_{\rm{i}} $ 与$ {\alpha }_{\rm{j}} $ 的区别。假设5：为方便计算，本文暂时忽略同一联盟内部各俱乐部目标函数的分歧，重点研究不同联盟工资帽政策的差异，因此可以假设权重：
$ {\alpha }_{\rm{i}}={\alpha }_{\rm{j}}=\alpha $ 。此时一阶条件（6）和（7）可简化为：
$$\frac{\left[\alpha (\sigma -2{w}_{\rm{i}})+\left(1-\alpha \right)\right]{x}_{\rm{j}}}{{\left({x}_{\rm{i}}+{x}_{\rm{j}}\right)}^{2}}=\alpha c$$ (11) $$ \frac{\left[\alpha (1-2{w}_{\rm{j}})+\left(1-\alpha \right)\right]{x}_{\rm{i}}}{{({x}_{\rm{i}}+{x}_{\rm{j}})}^{2}}=\alpha c$$ (12) 联立公式（8）、（11）、（12），解得：
$$ \left\{\begin{split} & {{x}_{\rm{i}}^{*}}=\frac{\left(2-3\alpha +\alpha \sigma \right){\left(1-\alpha +\alpha \sigma \right)}^{2}}{\alpha\left(g+z\right) {\left(2-\alpha +\alpha \sigma \right)}^{3}} > 0 \\&{{x}_{\rm{j}}^{*}}=\frac{\left(2-3\alpha +\alpha \sigma \right)\left(1-\alpha +\alpha \sigma \right)}{\alpha {\left(g+z\right)\left(2-\alpha +\alpha \sigma \right)}^{3}} > 0 \end{split} \right.$$ (13) $$\left\{ \begin{gathered} w_{\text{i}}^* = \frac{{1 + \alpha \left( {\sigma - 1} \right)}}{{2 + \alpha \left( {\sigma - 1} \right)}} \\ w_{\text{j}}^* = \frac{1}{{2 + \alpha \left( {\sigma - 1} \right)}} \\ \end{gathered} \right.$$ (14) $$ \frac{{{x}_{\rm{i}}^{*}}}{{{x}_{\rm{j}}^{*}}}=1+\alpha \left(\sigma -1\right)=\frac{{{w}_{\rm{i}}^{*}}}{{{w}_{\rm{j}}^{*}}} > 1 $$ (15) 需要注意的是，在上述简化中可以对
$ \dfrac{{{x}_{\rm{i}}^{*}}}{{{{x}}_{\mathrm{j}}^{*}}}、\dfrac{{{w}_{\rm{i}}^{*}}}{{{w}_{\rm{j}}^{*}}} $ 的大小进行判断，显然，$ \dfrac{{{x}_{\rm{i}}^{*}}}{{{{x}}_{\mathrm{j}}^{*}}}=\dfrac{{{w}_{\rm{i}}^{*}}}{{{w}_{\rm{j}}^{*}}}=1+\alpha \left(\sigma -1\right) > 1 $ 。性质3：当同一联盟中俱乐部胜率权重相同时，竞争性平衡是利润权重与俱乐部盈利能力差异的负相关函数；当俱乐部完全不关注利润或盈利能力相同时，可实现完全竞争性平衡。
2.1.4 俱乐部的反应函数图像
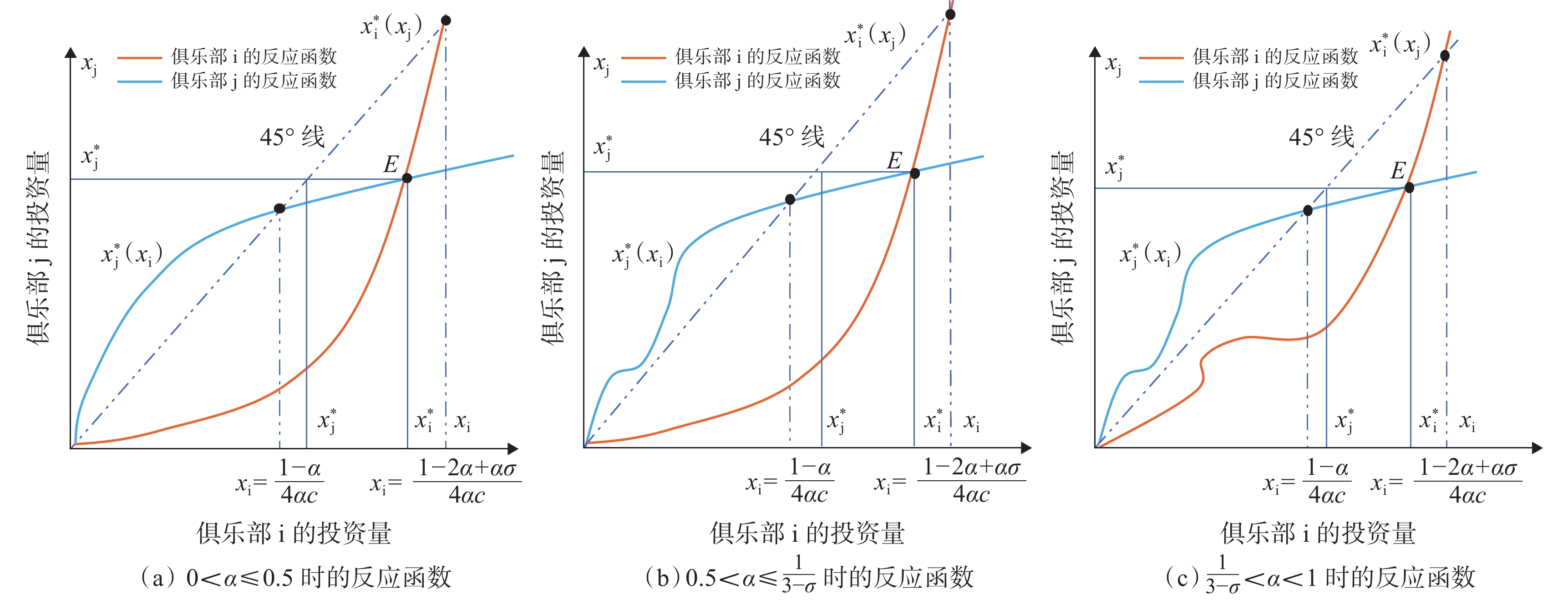
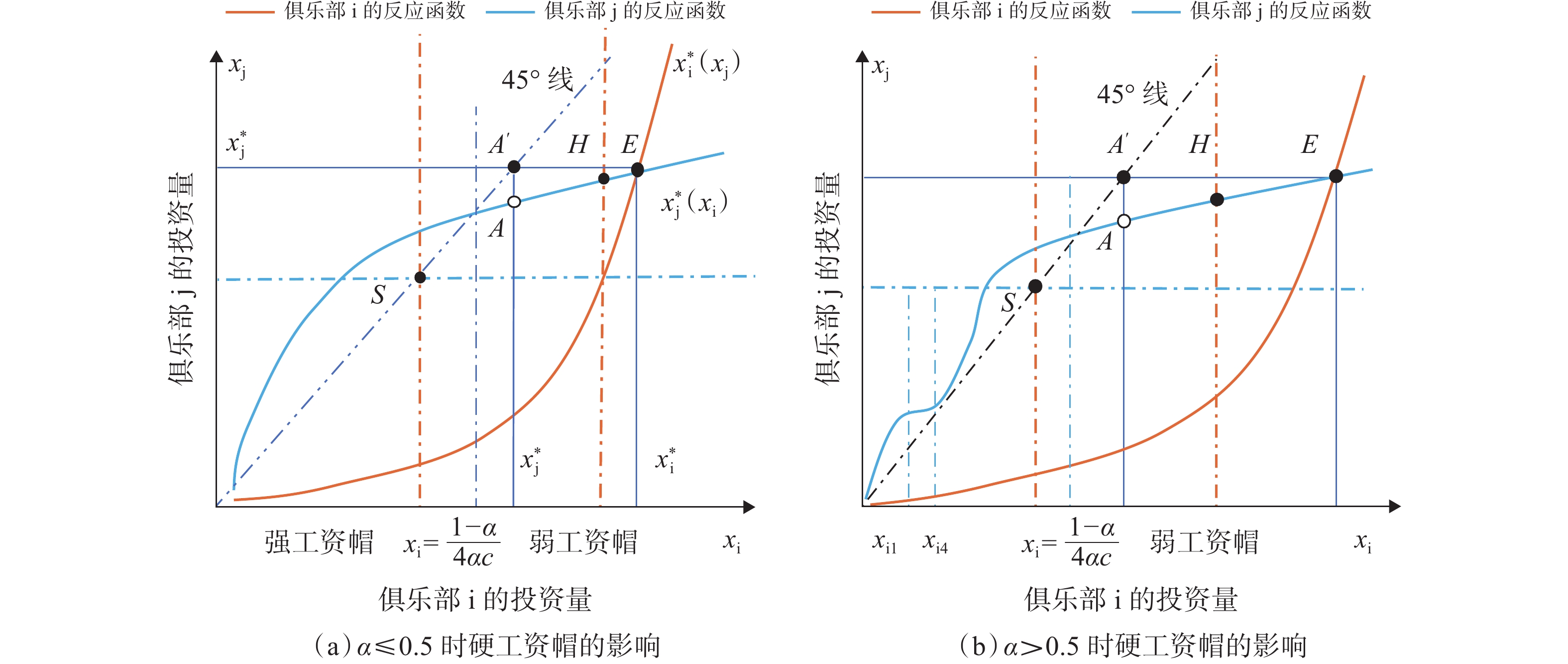
根据反应函数的凹凸性、与45°线的交点、与均衡解的位置关系，可以画出2个俱乐部的反应函数，如图2所示。其中：横、纵坐标轴分别表示俱乐部i、j的投资量
$ {x}_{\rm{i}} $ 和$ {x}_{\rm{j}} $ ；经过原点的曲线$ {x}_{\rm{i}}^{\mathrm{*}}\left({x}_{\rm{j}}\right) $ 和$ {x}_{\rm{j}}^{\mathrm{*}}\left({x}_{\rm{i}}\right) $ 表示无约束时俱乐部i、j的反应函数，其交点E为公式（13）所示无约束时的均衡解；2个俱乐部的均衡投资量分别为$ {x}_{\rm{i}}^{\mathrm{*}} $ 和$ {x}_{\rm{j}}^{\mathrm{*}} $ ；俱乐部i、j的反应函数与45°线的交点分别为$\left(\dfrac{1-\alpha }{4\alpha c},\dfrac{1-\alpha }{4\alpha c}\right)$ 和$\left(\dfrac{1-\mathrm{\alpha }+\mathrm{\alpha }\left(\mathrm{\sigma }-1\right)}{4\alpha c},\dfrac{1-\mathrm{\alpha }+\mathrm{\alpha }\left(\mathrm{\sigma }-1\right)}{4\alpha c}\right)$ 。可以发现，
$ \alpha $ 的取值范围决定了俱乐部反应函数的凹凸性。当$ 0 < \alpha \leqslant 0.5 $ 时，俱乐部j的反应函数恒为凹函数[图2（a）]；当$ \alpha > 0.5 $ 时，俱乐部j的反应函数则会出现一段凸函数[图2（b）、图2（c）]。当$\alpha \leqslant \dfrac{1}{3-\sigma }$ 时，俱乐部i的反应函数恒为凹函数；当$\dfrac{1}{3-\sigma } < \alpha < 1 $ 时，俱乐部i的反应函数会出现一段凸函数。无论凹凸性如何，无约束下的均衡点E总在45°线下方，即大城市俱乐部的均衡投资量总是大于小城市俱乐部。2.2 硬工资帽政策对俱乐部投资决策的影响
硬工资帽特指工资上限，对于工资下限暂不作讨论。软工资帽包括全额罚款（即如果工资支出超过奢侈税阈值，则支出多少就缴多少罚款，是一种比较严厉的税收方式）和差额罚款（即如果工资支出超过奢侈税阈值，则超过多少就缴多少，是一种较温和的税收方式）2种方式，本文主要讨论中超联赛与CBA联赛中所采用的差额罚款方式。
根据前文假设，在硬工资帽约束的情形下，俱乐部目标函数及其约束条件为：
$$\left\{\begin{split}\\ & {U}_{\rm{i}}=\left[\alpha (\sigma -{w}_{\rm{i}})+\left(1-\alpha \right)\right]{w}_{\rm{i}}-\alpha c{x}_{\rm{i}} \\&{U}_{\rm{j}}=\left[\alpha (1-{w}_{\rm{j}})+\left(1-\alpha \right)\right]{w}_{\rm{j}}-\alpha c{x}_{\rm{j}} \end{split}\right. $$ (16) $$ {\rm{s.t.}}\;\left\{\begin{split} & c{x}_{\rm{i}} \leqslant H\iff {x}_{\rm{i}} \leqslant \frac{H}{c}=G\\&c{x}_{\rm{j}} \leqslant H\iff {x}_{\rm{j}} \leqslant \frac{H}{c}=G \end{split} \right.$$ (17) 其中：H表示硬工资帽的货币限额，即名义工资帽；G表示施加在球员才能上的约束，即实际工资帽。
前文2.1.3已经证明在无约束条件下
$ {{x}_{\rm{j}}^{*}} < {{x}_{\rm{i}}^{*}} $ ，因此对俱乐部投资约束时有3种情况：①$ {{x}_{\rm{j}}^{*}} < {{x}_{\rm{i}}^{*}} \leqslant G $ ，约束无效，均衡为无约束解；②$ {{x}_{\rm{j}}^{*}} \leqslant G < {{x}_{\rm{i}}}^{\mathrm{*}} $ ，约束仅对俱乐部i产生作用；③$ G < {{{x}}_{\mathrm{j}}}^{\mathrm{*}} < {{x}_{\rm{i}}}^{\mathrm{*}} $ ，约束对2个俱乐部都起作用。由于目标函数是近似凹函数，后2种情况大城市俱乐部在约束下的均衡为$ {x}_{\rm{i}}=G $ 。由图2可知，在
$ \alpha =0.5 $ 与$ \alpha = \dfrac{1}{3-\sigma } $ 2个断点处，俱乐部i、j的反应函数会有显著变化，需分段讨论。文中所涉工资帽大多施加于大城市俱乐部，尤其在硬工资帽下大城市俱乐部的最优投资总是$ {x}_{\rm{i}}=G $ ，主要变动与分析首先与俱乐部j的反应函数相关，故本文以俱乐部j的断点$ \alpha =0.5 $ 为分段依据。2.2.1 当
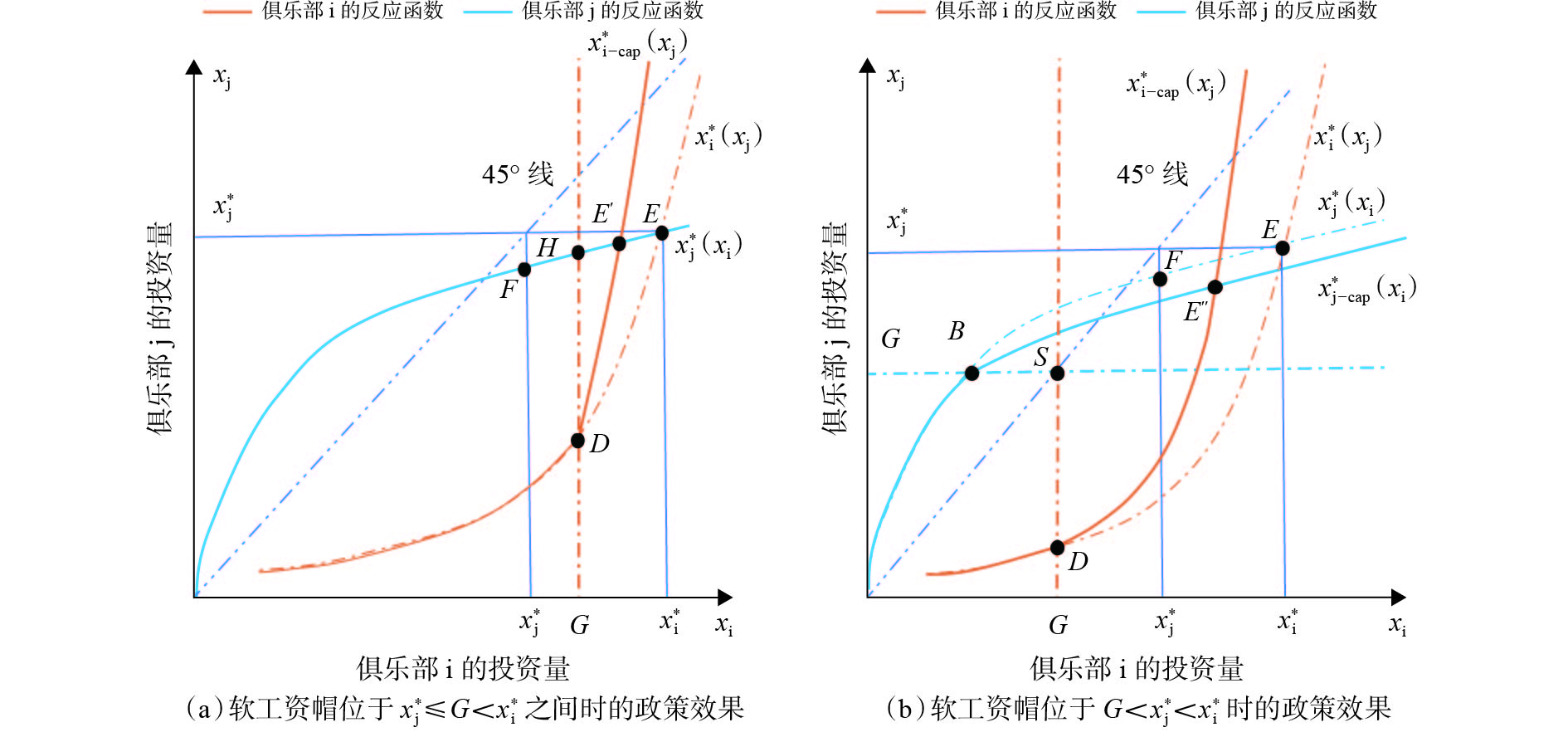
$ \mathit{\alpha } \leqslant 0.5 $ 时硬工资帽政策的影响图3的横纵坐标轴以及无约束均衡与图2完全一致。E点为无约束时的均衡解，H点为工资帽约束较弱时的均衡解，S点为强工资帽约束下的均衡解，
$A $ 和$ {A}^{\prime} $ 点为工资帽$ G={x}_{\rm{j}}^{\mathrm{*}} $ 时的均衡解。![]()
图 3 硬工资帽对俱乐部投资决策与联盟竞争性平衡的影响Figure 3. The influence of hard salary cap on clubs' investment decision and league's competitive balance可以发现，如果
$ \sigma $ 较小即俱乐部盈利能力差异较小时，俱乐部j的反应函数极值点在均衡点右侧，此时随着工资帽阈值下降会先对俱乐部i进行限制，然后从$ G={{x}_{\rm{j}}}^{*} $ 开始对2个俱乐部同时施加限制。在这一过程中：俱乐部i的投资始终减少；俱乐部j的投资总体呈递减趋势，但在$ G={{x}_{\rm{j}}}^{*} $ 时会向上跳跃，因此在略小于小城市俱乐部无约束均衡时，工资帽在限制俱乐部j的投资上无效；竞争性平衡以递减的速度逐渐提高，最终在$ G={{x}_{\rm{j}}}^{*} $ 时实现完全竞争。如果$ \sigma $ 较大，则俱乐部j的反应函数极值点在无约束均衡点左侧，此时随着工资帽阈值下降，俱乐部i的投资量始终在减少；但俱乐部j的投资不仅在$ G={{x}_{\rm{j}}}^{*} $ 时会出现跳跃，在极值点右侧也一直上升，即工资帽政策此时并没有对俱乐部j的投资量产生限制作用；联盟竞争性平衡也始终变大，且其变化速度先减小后增大。2.2.2 当
$ \mathit{\alpha } > 0.5 $ 时硬工资帽政策的影响当
$ \alpha > 0.5 $ 时，俱乐部j的反应函数不再是完全的凹函数，而是在45°线左侧出现一段凸函数（$ {x}_{\rm{i}}={x}_{{\rm{i}}4} $ 附近）。已证明极小值点$ \left({x}_{{\rm{i}}4},{x}_{{\rm{j}}4}\right) $ 处在45°线的左侧，而无约束均衡点在45°线右侧，因此反应函数在45°线右侧部分的整体趋势与$ \alpha < 0.5 $ 时的情况基本一致，此时工资帽政策对俱乐部投资的影响与$ \alpha < 0.5 $ 时完全相同。具体到$0.5 < \alpha < \dfrac{1}{3 - \sigma }$ 与$\dfrac{1}{3 - \sigma } < \alpha < 1$ ，硬工资帽的政策效果也基本无差异。命题1。①无论联盟中俱乐部更重视胜率还是利润，硬工资帽政策总能促进竞争性平衡，且在阈值小于小城市俱乐部的无约束均衡时实现完全竞争。②俱乐部j的最优投资变化与俱乐部盈利能力的差距相关：当差距较大时，俱乐部j的最优投资水平会随工资帽阈值的减小而先上升后下降，即在投资的边际成本不变时，小城市俱乐部投资的边际收入对大城市俱乐部投资的偏导数小于零；当差距较小时，俱乐部j的最优投资水平随工资帽阈值的减小逐渐减小。③俱乐部j的最优投资在工资帽阈值刚好等于
$ {{x}_{\rm{j}}}^{\mathrm{*}} $ 时出现向上跳跃，因此在限制投资的政策目标下，工资帽阈值要避免设置在略小于等于小城市俱乐部无约束均衡处。2.3 软工资帽政策对俱乐部投资决策的影响
本文重点讨论差额罚款情形，即当俱乐部工资支出超过奢侈税起征点后，超过部分需缴纳一定比例罚款（事实上全额罚款与差额罚款类似，只是罚款比例变为
$ t+1 $ ，本文不作单独分析）。以下讨论CBA工资帽与中超联赛引援调节费政策中采用的固定税率，暂不考虑NBA和MLB中的累进税率（累进税的政策效果处于一个较大固定税率与较小固定税率之间，可参见Fu等[29]的研究）。在差额罚款、固定税率的软工资帽政策下，俱乐部i的最优目标函数及其约束条件可表示为：
$$ {U}_{\rm{i}}=\left[\alpha (\sigma -{w}_{\rm{i}})+\left(1-\alpha \right)\right]{w}_{\rm{i}}-\alpha c{x}_{\rm{i}}-t\alpha c\left({x}_{\rm{i}}-G\right)\cdot {\mathbb{I}}_{{x}_{\rm{i}}\geqslant G} $$ (18) 其中：示性函数
$ {\mathbb{I}}_{{x}_{\rm{i}}\geqslant G} $ 表示当且仅当$ {x}_{\rm{i}}\geqslant G $ 时，$ \alpha c\left({x}_{\rm{i}}-G\right) $ 项才存在；t表示奢侈税的税率。在无约束模型中已解得
$ {{x}_{\rm{i}}^{*}} > {{{x}}_{\mathrm{j}}^{*}} > 0 $ ，因此对俱乐部进行软工资帽约束时会出现3种情况：（1）如果
${{x}_{\rm{j}}^{*}} < {{x}_{\rm{i}}^{*}}\leqslant G$ ，约束条件不起作用，最优解为无约束下的均衡解。（2）如果
${{{x}}_{\mathrm{j}}^{\mathrm{*}}}\leqslant G < {{x}_{\rm{i}}^{\mathrm{*}}}$ ，约束条件仅对俱乐部i起作用，此时的目标函数为：$$\left\{ \begin{gathered} {U_{\text{i}}} = \left[ {\alpha (\sigma - {w_{\text{i}}}) + \left( {1 - \alpha } \right)} \right]{w_{\text{i}}} - \left( {1 + t} \right)\alpha c{x_{\text{i}}} + t\alpha cG \\ {U_{\text{j}}} = \left[ {\alpha (1 - {w_{\text{j}}}) + \left( {1 - \alpha } \right)} \right]{w_{\text{j}}} - \alpha c{x_{\text{j}}} \\ \end{gathered} \right. $$ (19) 一阶条件FOC整理得：
$$\left\{ \begin{gathered} \frac{{\partial {U_{\text{i}}}}}{{\partial {x_{\text{i}}}}} = \left[ {\alpha \left( {\sigma - 2\frac{{{x_{\text{i}}}}}{{{x_{\text{i}}} + {x_{\text{j}}}}}} \right) + \left( {1 - \alpha } \right)} \right]\frac{{{x_{\text{j}}}}}{{{{\left( {{x_{\text{i}}} + {x_{\text{j}}}} \right)}^2}}} - \left( {1 + t} \right)\alpha c = 0 \\ \frac{{\partial {U_{\text{j}}}}}{{\partial {x_{\text{j}}}}} = \left[ {\alpha \left( {1 - 2\frac{{{x_{\text{j}}}}}{{{x_{\text{i}}} + {x_{\text{j}}}}}} \right) + \left( {1 - \alpha } \right)} \right]\frac{{{x_{\text{i}}}}}{{{{\left( {{x_{\text{i}}} + {x_{\text{j}}}} \right)}^2}}} - \alpha c = 0 \\ \end{gathered} \right.$$ (20) 对于俱乐部j，其反应函数与无约束时相同。对于俱乐部i，在
$ {x}_{\rm{i}}\leqslant G $ 时与无约束时相同，但当$ {x}_{\rm{i}} > G $ 时反应函数左边最后一项由$ -\alpha \mathrm{c} $ 变为$ -\left(1+t\right)\alpha \mathrm{c} $ 。以$ \alpha < 0.5 $ 为例，此时函数会由图3（a）调整为图4（a）。其中，$ {x}_{\rm{j}}^{\mathrm{*}}\left({x}_{\rm{i}}\right) $ 为俱乐部j的反应函数曲线，虚线$ {x}_{\rm{i}}^{\mathrm{*}}\left({x}_{\rm{j}}\right) $ 是俱乐部i无约束时的反应函数曲线，交点E为均衡解，与图3（a）完全一致。点H为硬工资帽下的均衡解，也与图3（a）一致。$ {x}_{{\rm{i-cap}}}^{\mathrm{*}}\left({x}_{\rm{j}}\right) $ 表示软工资帽下俱乐部i的反应函数，其与$ {x}_{\rm{i}}^{\mathrm{*}}\left({x}_{\rm{j}}\right) $ 在D点左侧完全重合，但在D点右侧斜率更大，与俱乐部j的反应函数$ {x}_{\rm{j}}^{\mathrm{*}}\left({x}_{\rm{i}}\right) $ 的交点$ {E}{{'}} $ 为软工资帽下的均衡解。![]()
图 4 软工资帽对俱乐部投资决策与联盟竞争性平衡的影响Figure 4. The influence of soft salary cap on clubs' investment decisions and league's competitive balance可以发现：相较于无约束时的均衡点E，在软工资帽下的均衡点
$ {E}{{'}} $ 处，2个俱乐部的最优投资量均减少，且由于其到45°线的距离更近，竞争性平衡也有所提高；相较于硬工资帽下的均衡点H，2个俱乐部的最优投资量都减少得更多，且由于其到45°线的距离比H更远，对竞争性平衡的促进作用也更小。命题2。当软工资帽约束力度较小时（即阈值处于2个俱乐部无约束均衡之间）：①随着工资帽阈值减小（直至
$ G={x}_{\rm{j}}^{\mathrm{*}} $ ），2个俱乐部的均衡投资量都减少，但竞争性平衡增大，工资帽政策有效；②软工资帽对俱乐部均衡投资量的抑制作用不如硬工资帽，且对竞争性平衡的促进作用也劣于硬工资帽。（3）如果
$ G < {{x}_{\rm{j}}^{\mathrm{*}}} < {{x}_{\rm{i}}^{\mathrm{*}}} $ ，政策对2个俱乐部都起作用。此时的反应函数为：$$\left\{ \begin{gathered} \frac{{\partial {U_{\text{i}}}}}{{\partial {x_{\text{i}}}}} = \left[ {\alpha \left( {\sigma - 2\frac{{{x_{\text{i}}}}}{{{x_{\text{i}}} + {x_{\text{j}}}}}} \right) + \left( {1 - \alpha } \right)} \right]\frac{{{x_{\text{j}}}}}{{{{\left( {{x_{\text{i}}} + {x_{\text{j}}}} \right)}^2}}} - \left( {1 + t} \right)\alpha c = 0 \\ \frac{{\partial {U_{\text{j}}}}}{{\partial {x_{\text{j}}}}} = \left[ {\alpha \left( {1 - 2\frac{{{x_{\text{j}}}}}{{{x_{\text{i}}} + {x_{\text{j}}}}}} \right) + \left( {1 - \alpha } \right)} \right]\frac{{{x_{\text{i}}}}}{{{{\left( {{x_{\text{i}}} + {x_{\text{j}}}} \right)}^2}}} - \left( {1 + t} \right)\alpha c = 0 \\ \end{gathered} \right.$$ (21) 反应函数图像如图4（b）所示。其中，E仍表示无约束时的均衡点，虚线
$ {x}_{\rm{i}}^{\mathrm{*}}\left({x}_{\rm{j}}\right) $ 和$ {x}_{\rm{j}}^{\mathrm{*}}\left({x}_{\rm{i}}\right) $ 表示无约束时2个俱乐部的反应函数曲线。粗实线$ {x}_{{\rm{i-cap}}}^{\mathrm{*}}\left({x}_{\rm{j}}\right) $ 表示软工资帽约束下俱乐部i的反应函数，其在D点左侧与无约束时的反应函数相同，但在右侧时斜率变大。粗实线$ {x}_{{\rm{j-cap}}}^{\mathrm{*}}\left({x}_{\rm{i}}\right) $ 表示软工资帽约束下俱乐部j的反应函数，其在B点左侧与无约束时的反应函数相同，但在右侧时斜率变小。工资帽约束下新的均衡点为$ {E}^{\prime\prime} $ 。可以发现，此时2个俱乐部的反应函数是等比例移动的，因此均衡投资量也等比例减少，故竞争性平衡与无约束时相同。前文已知工资帽处于
$ {{x}_{\rm{j}}}^{*}\leqslant G < {{x}_{\rm{i}}}^{*} $ 时，随着阈值减小均衡点由E移动到F，竞争性平衡逐渐增加。在$ G < x_{\text{j}}^* < x_{\text{i}}^* $ 时，${E}^{\prime\prime} $ 的竞争性平衡又等于无约束均衡，因此在F点存在突变，即当软工资帽阈值过低时，其在促进竞争性平衡上失效。此时的政策效果也远远不如硬工资帽的均衡点S。命题3。当软工资帽约束力度较大时（即阈值小于小城市俱乐部无约束解），此工资帽政策对竞争性平衡无任何促进作用，对俱乐部投资额有一定的抑制作用，但其效果又远低于硬工资帽的政策效果。
3. 研究结论、政策启示和未来展望
3.1 研究结论
本文以竞赛理论为基础，通过博弈论与静态优化方法，分析了在考虑收益内生和俱乐部目标函数差异情况下，俱乐部软、硬工资帽政策的适用条件及其对俱乐部最优投资和竞争性平衡的影响。对无约束条件均衡与工资帽限制下的俱乐部最优投资均衡进行比较可以发现：
（1）在硬工资帽政策约束下，无论联盟中俱乐部更看重胜率还是利润：①如果俱乐部盈利能力的差距较大，那么硬工资帽政策对2个俱乐部都会起作用，且随着工资帽临界值的降低，大城市俱乐部的均衡投资一直降低，而小城市俱乐部的均衡投资可能会先上升再降低；②如果俱乐部盈利能力差距较小，那么随着工资帽临界值的降低，所有俱乐部的均衡投资都将始终降低；③无论俱乐部盈利能力差距多大，联盟的竞争性平衡总是在增加，直至工资帽阈值小于等于小城市俱乐部无约束均衡时实现完全竞争。
（2）在软工资帽政策约束下，如果政策规制力度不太大（即工资帽处于2个俱乐部无约束最优解之间），那么：①随着工资帽临界值的降低，2个俱乐部的均衡取值都降低，且竞争性平衡增大；②相较于硬工资帽下的均衡而言，软工资帽政策下2个俱乐部投资量的减少更小，且对竞争性平衡的促进作用也不如硬工资帽；③如果政策规制力度较大（即工资帽临界值比无约束时小城市俱乐部投资额小），随着工资帽临界值的降低，2个俱乐部的均衡投资量均减少，而竞争性平衡在工资帽临界值刚好等于小城市俱乐部无约束均衡投资时会出现一个断崖式下降，此后相对于无约束时的竞争性平衡没有任何变化。因此，如果政策目标是提高联盟竞争性平衡，那么工资帽的临界值不能设置得太小（必须要大于小城市俱乐部无约束时的均衡投资）。
3.2 对中国职业体育联盟的政策启示
3.2.1 进一步完善硬工资帽政策的制定与实施，审慎选择软工资帽政策
无论俱乐部更看重胜率还是利润，硬工资帽都可以有效促进竞争性平衡，降低大城市俱乐部投资，但对小城市俱乐部投资的作用不太明确；软工资帽政策只有在不太严格的临界值下才会促进竞争性平衡与限制投资，但效果总是次于硬工资帽政策。同时，梳理软、硬工资帽政策的演进历史发现，硬工资帽政策在封闭式联盟与开放式联盟中都有广泛应用，而软工资帽政策主要出现在封闭式联盟中，且还搭配了选秀、收益共享等制度共同使用才可能起到作用。因此，对于中超联赛而言，当前实行的硬工资帽政策是一种较好选择，但也还需要在维持竞争性平衡与保证俱乐部绝对质量（人才投资总额）之间做好权衡，其临界值至少不能低于无约束时小城市俱乐部的均衡投资额，否则就会在牺牲俱乐部有效投资的同时降低联赛的竞争性平衡。对于CBA而言，虽然在联盟组织形式上其是类似NBA的一种封闭式联盟，但CBA俱乐部并非都与NBA俱乐部一样追求利润最大化，且联盟的市场结构也存在显著差异（CBA上游还有中国篮协的监管，并非俱乐部自治型联盟），因此当前实施软工资帽政策并不一定会有效，即使有效也明显劣于硬工资帽政策。
总体而言，无论对于中超联赛还是CBA，如果联盟政策规制的首要目标是降低俱乐部的总支出、抑制“金元体育”背景下投资人的非理性投资、提高联盟的竞争性平衡，那么工资帽政策尤其是硬工资帽政策可以较好地达到预期效果。在具体的操作层面：①对于存在“金元泡沫”与控股股东“非理性投资”的联盟，要加快制定、出台工资帽政策；②在政策实施过程中，也要有效防止俱乐部利用球员肖像权合同或关联公司的广告等冲抵工资、奖金以规避工资帽政策的监管，同时还需要对俱乐部财务严格审查，及时公开俱乐部财务情况，统一球员薪酬发放的银行账户，加强俱乐部合同的备案审查等。
3.2.2 推进俱乐部股权多元化结构性改革，合理控制胜率最大化和利润最大化股东比例
如果联盟中的俱乐部都更重视利润，则所有俱乐部的均衡投资量都会更小，但联盟竞争性平衡会更差；但如果俱乐部更重视胜率，则所有俱乐部的均衡投资量会更大，且联盟竞争性平衡也更好。基于这一结论不难发现，更多的俱乐部投资和更好的联盟竞争性平衡更有利于推动联盟发展壮大。因此，在联盟快速发展阶段会更偏好提高俱乐部的胜率。在这一动机驱使下，职业体育俱乐部中极有可能会出现一批不看重俱乐部本身利润，而看重球队获胜带来的心理喜悦以及对关联产业推动作用的赞助商和投资人。这也正符合2011年以来中超俱乐部中民营房地产企业或涉房地产企业通过投资足球俱乐部来获得政治回报和其他产业加成的客观现实[57-58]。如果大量民营房企控股职业体育俱乐部，那么行业结构单一的问题会变得非常突出，隐含风险也会增大，一旦该行业面临大环境冲击就极易出现俱乐部营运难以为继的现象[58]，继而造成球员欠薪和俱乐部破产等后果。
为了保证联盟的发展和良好的运行生态，首先要明确，引入胜率最大化投资者的总体方向是肯定的，但同时也须充分考虑在新冠病毒感染疫情（以下简称“疫情”）与中国足球大环境恶化冲击下俱乐部破产风险激增的严峻现实，因而还必须保证一定比例的利润最大化投资者从内部对俱乐部财务状况进行约束。总体而言，中国职业体育联盟需要进一步推进股权多元化结构改革，不仅需要房地产企业与忠实球迷这种考虑胜率的投资者，还要引进基金投资和股票投资等价值投资者。同时要及时完善制约改革的相关规定，如取消《中国足球协会职业足球俱乐部转让规定》中关于“重要转让中的受让方必须是企业法人”的规定，否则将极大地限制有实力的自然人投资职业足球俱乐部，在很大程度上阻碍俱乐部股权多元化改革的推进。
3.2.3 有效把控工资帽政策规制力度，主动应对疫情冲击下的球员欠薪、球队破产等问题
疫情的冲击使职业体育赛事大量中断，门票与电视转播收入也急剧下降，同时还极大地冲击了赞助商的其他产业，使其减少对职业体育俱乐部的投入，最终造成了联赛收入进一步恶化、球员欠薪与球队破产等问题，严重损害中国职业体育市场的根基。在这种形势下，如何保证俱乐部生存与联盟的可持续发展成为“后疫情”时期改革的重点。要实现这一目标，一是节流，二是开源。
（1）在节流方面，职业体育俱乐部最主要的支出是球员工资和转会费，因此进一步推行工资帽和转会帽（即引援调节费政策）等、降低球员薪资是最切实有效的途径。同时也要注意把握好降低球员薪资的尺度，不能因工资过低而使得大量优质球员流失或消极对待比赛。
（2）在开源方面，在联盟直接收入受疫情冲击的情况下，改善联赛投资环境、提升投资人的投资热情是关键举措。对于中国职业体育而言，应及时调整“中性名”等政策，提高赞助商投资职业足球俱乐部的价值回报。在鼓励投资的同时，也要积极拓展俱乐部的其他收入来源，防止因为收入结构的过度单一而加剧俱乐部破产倒闭的风险。
3.3 研究不足与未来展望
（1）本文考虑的是一个俱乐部自治型联盟，即俱乐部通过横向协议组成的一个战略性联盟。在这种市场结构中，只存在俱乐部策略性决策，联盟无决策权，因此联盟的规制事实上是俱乐部自治。但在很多开放式联盟（如中超联赛）中，足球协会对职业联赛的影响非常大，其作为一个垄断性实体为职业体育赛事提供基础服务，其下游的竞争性俱乐部则利用协会提供的平台和中间商品并结合俱乐部自身的球员投入联合生产赛事产品。因此，上游协会对理论模型的构建与研究结果都可能产生较大影响，后期研究可以进一步加入上游协会。
（2）本文主要讨论了俱乐部层次的工资帽政策对俱乐部总投资和竞争性平衡的影响，但职业体育联盟的交叉补贴政策不仅包括俱乐部总体的工资帽，也存在针对单个球员的工资帽，且不仅包括工资帽还包括亏损帽（即欧足联的盈亏平衡准则FFP）、转会帽等规制政策。同时，不同的交叉补贴政策对俱乐部投资的影响途径与影响力度都不同，相互搭配使用时是否会出现一些预料外的结果也值得进一步研究。
（3）本文从理论上对工资帽政策进行推导，没有使用实际数据进行检验。事实上，如果有高质量的联盟投入产出数据，也可以通过结构模型先准确估计影响竞赛胜率与效用函数的基本参数，然后通过对回归模型施加约束，模拟各种交叉补贴政策在不同联盟中对俱乐部投资决策与联盟竞争的影响。
总体而言，本文从产业组织理论与应用微观经济学角度出发，为职业体育联盟的组织与规制提供了一种新思路，对后续研究有一定借鉴作用。
作者贡献声明：周腾军：设计论文框架，推导数学模型，撰写论文；作者贡献声明：郑朝南：推导数学模型，进行数值模拟，撰写、修改论文；作者贡献声明：靳厚忠：提出论文主题，设计论文框架，修改论文。 -
![]()
图 1 职业体育联盟中硬工资帽政策的演进历程
Figure 1. The history of hard salary cap policies in professional sports leagues
![]()
图 3 硬工资帽对俱乐部投资决策与联盟竞争性平衡的影响
Figure 3. The influence of hard salary cap on clubs' investment decision and league's competitive balance
![]()
图 4 软工资帽对俱乐部投资决策与联盟竞争性平衡的影响
Figure 4. The influence of soft salary cap on clubs' investment decisions and league's competitive balance
表 1 国内外不同联赛工资帽政策选择与实施情况对比
Table 1 Comparison of salary cap policies and implementation in different leagues
联盟 俱乐部层次 球员层次 工资上限 工资下限 奢侈税 硬工资帽 NBA YES YES YES YES NFL YES NO NO NO MLB YES NO YES NO NHL YES YES NO NO EPL YES NO NO NO La Liga YES NO NO NO CSL YES NO NO YES CBA YES YES YES YES 注：只有工资上下限而没有奢侈税是硬工资帽政策，既有工资上下限又有奢侈税是软工资帽政策。 
下载: 导出CSV
-
[1] DOBSON S,GODDARD J. Performance,revenue,and cross subsidization in the football league,1927-1994[J]. The Economic History Review,1998,51(4):763-785 doi: 10.1111/1468-0289.00113
[2] DOWNWARD P, DAWSON A. The economics of professional team sports[M]. London: Routledge, 2000
[3] FORT R,QUIRK J. Cross-subsidization,incentives,and outcomes in professional team sports leagues[J]. Journal of Economic Literature,1995,33(3):1265-1299 doi: 10.2307/2729122
[4] BOOTH R. Comparing competitive balance in Australian sports leagues:Does a salary cap and player draft measure up?[J]. Sport Management Review,2005,8(2):119-143 doi: 10.1016/S1441-3523(05)70036-X
[5] CHATZISTAMOULOU N,KOSTAS K,THEODOR A. Salary cap,organizational gap,and catch-up in the performance of NBA teams:A two-stage DEA model under heterogeneity[J]. Journal of Sports Economics,2022,23(2):123-155 doi: 10.1177/15270025211022253
[6] KESENNE S. The impact of salary caps in professional team sports[J]. Scottish Journal of Political Economy,2000,47(4):422-430 doi: 10.1111/1467-9485.00171
[7] KESENNE S. The salary cap proposal of the G-14 in European football[J]. European Sport Management Quarterly,2003,3(2):120-128 doi: 10.1080/16184740308721944
[8] LARSEN A,FENN A J,SPENNER E L. The impact of free agency and the salary cap on competitive balance in the national football league[J]. Journal of Sports Economics,2006,7(4):374-390 doi: 10.1177/1527002505279345
[9] VROOMAN J. A general theory of professional sports leagues[J]. Southern Economic Journal,1995,61(4):971-990 doi: 10.2307/1060735
[10] TULLOCK G. Efficient rent seeking[M]// TOLLISON B R, TULLOCK G. Toward a theory of rent seeking society. Texas: Texas A&M University Press, 1980
[11] LAZEAR E P,ROSEN S. Rank-order tournaments as optimum labor contracts[J]. Journal of Political Economy,1981,89(5):841-864 doi: 10.1086/261010
[12] KONRAD K A. Strategy and dynamics in contests[M]. Oxford U.K.: Oxford University Press, 2009
[13] BAIK K H. Effort levels in contests with two asymmetric players[J]. Southern Economic Journal,1994,61(2):367-378 doi: 10.2307/1059984
[14] CHUNG T Y. Rent-seeking contest when the prize increases with aggregate efforts[J]. Public Choice,1996,87(1/2):55-66 doi: 10.1007/BF00151729
[15] DIXIT A. Strategic behavior in contests:Reply[J]. American Economic Review,1999,89(3):694 doi: 10.1257/aer.89.3.694
[16] FU Q,LU J F. Contest with pre-contest investment[J]. Economics Letters,2009,103(3):142-145 doi: 10.1016/j.econlet.2009.03.011
[17] GELDER A,KOVENOCK D. Dynamic behavior and player types in majoritarian multi-battle contests[J]. Games and Economic Behavior,2017,104:444-455 doi: 10.1016/j.geb.2017.05.008
[18] SZYMANSKI S. The economic design of sporting contests[J]. Journal of Economic Literature,2003,41(4):1137-1187 doi: 10.1257/jel.41.4.1137
[19] GROSSMANN M,DIETL H. Investment behaviour in a two-period contest model[J]. Journal of Institutional and Theoretical Economics,2009,165(3):401-417 doi: 10.1628/093245609789471998
[20] DIETL H M,FRANCK E. Governance failure and financial crisis in German football[J]. Journal of Sports Economics,2007,8(6):662-669 doi: 10.1177/1527002506297022
[21] DIETL H M,FRANCK E,LANG M. Overinvestment in team sports leagues:A contest theory model[J]. Scottish Journal of Political Economy,2008,55(3):353-368 doi: 10.1111/j.1467-9485.2008.00457.x
[22] LEACH S,SZYMANSKI S. Making money out of football[J]. Scottish Journal of Political Economy,2015,62(1):25-50 doi: 10.1111/sjpe.12065
[23] CHE Y K,GALE I L. Caps on political lobbying[J]. American Economic Review,1998,88(3):643-651 doi: 10.1257/000282806779468490
[24] CHE Y K,GALE I L. Caps on political lobbying:Reply[J]. American Economic Review,2006,96(4):1355-1360 doi: 10.1257/aer.96.4.1355
[25] GAVIOUS A,MOLDOVANU B,SELA A E. Bid costs and endogenous bid caps[J]. The RAND Journal of Economics,2002,33(4):709-722 doi: 10.2307/3087482
[26] SAHUGUET N. Caps in asymmetric all-pay auctions with incomplete information[J]. Economics Bulletin,2006,3(9):1-8
[27] KAPLAN T R,WETTSTEIN D. Caps on political lobbying:Comment[J]. American Economic Review,2006,96(4):1351-1354 doi: 10.1257/aer.96.4.1351
[28] OLSZEWSKI W,SIEGEL R. Bid caps in large contests[J]. Games and Economic Behavior,2019,115:101-112 doi: 10.1016/j.geb.2019.02.012
[29] FU Q, WU Z, ZHU Y. Optimal bid caps in noisy contests[J/OL]. American Economic Journal-Microeconomics[2022-03-02]. https://scholarbank.nus.edu.sg/handle/10635/227159
[30] SZYMANSKI S,KÉSENNE S. Competitive balance and gate revenue sharing in team sports[J]. The Journal of Industrial Economics,2004,52(1):165-177 doi: 10.1111/j.0022-1821.2004.00220.x
[31] PEETERS T,SZYMANSKI S. Financial fair play in European football[J]. Economic Policy,2014,29(78):343-390 doi: 10.1111/1468-0327.12031
[32] ROTTENBERG S. The baseball players' labor market[J]. Journal of Political Economy,1956,64(3):242-258 doi: 10.1086/257790
[33] GUSTAFSON E, HADLEY L. The luxury tax proposal for Major League Baseball: A partial equilibrium analysis[M]// FIZEL J, GUSTAFSON E, HADLEY L. Baseball economics: Current research. Westport: Praeger, 1996, 145-157
[34] MARBURGER D R. Gate revenue sharing and luxury taxes in professional sports[J]. Contemporary Economic Policy,1997,15(2):114-123 doi: 10.1111/j.1465-7287.1997.tb00471.x
[35] GUSTAFSON E. The luxury tax in professional sports[M]// ANDREFF W, SZYMANSKI S. Handbook on the economics of sport. UK: Edward Elgar Publishing Ltd., 2006
[36] DIETL H M,LANG M,WERNER S. The effect of luxury taxes on competitive balance,club profits,and social welfare in sports leagues[J]. International Journal of Sport Finance,2010,5(1):41-51
[37] MAXCY J G. The effect on player transfers of a luxury tax on club payrolls: The case of Major League Baseball[M]//ANDREFF W. Sports economics: Participation, events, and professional team sports. Cheltenham, UK and Northampton, MA, US: Edward Elgar, 2011: 80-92
[38] ROSEN S. Prizes and incentives in elimination tournaments[J]. American Economic Review,1986,76(4):701-715
[39] SKAPERDAS S. Contest success functions[J]. Economic Theory,1996,7(2):283-290 doi: 10.1007/BF01213906
[40] DIETL H, FRANCK E, LANG M, et al. Welfare effects of salary caps in sports leagues with Win-Maximizing clubs[R]. Working Paper（No. 08-25）of North American Association of Sports Economics , 2008
[41] GROSSMANN M,DIETL H. Asymmetric contests with liquidity constraints[J]. Public Choice,2012,150(3/4):691-713
[42] DIETL H M,GROSSMANN M,LANG M. Competitive balance and revenue sharing in sports leagues with utility-maximizing teams[J]. Journal of Sports Economics,2011,12(3):284-308 doi: 10.1177/1527002511404787
[43] KÉSENNE S. League management in professional team sports with win maximizing clubs[J]. Journal of Sports Economics,1996,1:56-65
[44] MADDEN P. Fan welfare maximization as a club objective in a professional sports league[J]. European Economic Review,2012,56(3):560-578 doi: 10.1016/j.euroecorev.2011.12.006
[45] QUIRK J P, EL-HODIRI M M. The economic theory of a professional sports league[M]// NOLL R G. Government and the sports business. Washington, DC: The Brookings Institution, 1974
[46] SLOANE P J. The economics of professional football:The football club as a utility maximiser[J]. Scottish Journal of Political Economy,1971,18(2):121-146 doi: 10.1111/j.1467-9485.1971.tb00979.x
[47] EL-HODIRI M,QUIRK J. An economic model of a professional sports league[J]. Journal of Political Economy,1971,79(6):1302-1319 doi: 10.1086/259837
[48] GARCIA-DEL-BARRIO P,SZYMANSKI S. Goal! Profit maximization versus win maximization in soccer[J]. Review of Industrial Organization,2009,34(1):45-68 doi: 10.1007/s11151-009-9203-6
[49] LANG M,GROSSMANN M. The sugar daddy game:How wealthy investors change competition in professional team sports[J]. Journal of Institutional and Theoretical Economics,2011,167(4):557-577 doi: 10.1628/jite-2011-0002
[50] FRANCK E. Private firm,public corporation or member's association–governance structures in European football[J]. International Journal of Sport Finance,2010,5(2):108-127
[51] HAMIL S,MORROW S,IDLE C,et al. The governance and regulation of Italian football[J]. Soccer & Society,2010,11(4):373-413
[52] ROHDE M,BREUER C. Competing by investments or efficiency? Exploring financial and sporting efficiency of club ownership structures in European football[J]. Sport Management Review,2018,21(5):563-581 doi: 10.1016/j.smr.2018.01.001
[53] ROHDE M,BREUER C. The market for football club investors:A review of theory and empirical evidence from professional European football[J]. European Sport Management Quarterly,2017,17(3):265-289 doi: 10.1080/16184742.2017.1279203
[54] ROHDE M,BREUER C. The financial impact of (foreign) private investors on team investments and profits in professional football:Empirical evidence from the premier league[J]. Applied Economics and Finance,2016,3(2):243-255 doi: 10.11114/aef.v3i2.1366
[55] FRANCK E,LANG M. A theoretical analysis of the influence of money injections on risk taking in football clubs[J]. Scottish Journal of Political Economy,2014,61(4):430-454 doi: 10.1111/sjpe.12052
[56] MADDEN P. Welfare economics of "financial fair play" in a sports league with benefactor owners[J]. Journal of Sports Economics,2015,16(2):159-184 doi: 10.1177/1527002512465759
[57] 王裕雄,靳厚忠. 中超联赛俱乐部持有人特征及动机判断:兼论职业足球俱乐部治理结构的选择[J]. 体育科学,2016,36(9):90-97 doi: 10.16469/j.css.201609014 [58] 鲍明晓. 我国职业足球俱乐部股权多元化改革的理论分析与推进策略[J]. 北京体育大学学报,2021,44(10):14-21 doi: 10.19582/j.cnki.11-3785/g8.2021.10.002 -
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 493
- HTML全文浏览量: 136
- PDF下载量: 77
- 被引次数: 1
目录
1. 工资帽政策的制度演进
1.1 硬工资帽政策的制度演进
1.2 软工资帽政策的制度演进
1.3 国内外软、硬工资帽政策的比较
2. 工资帽政策的作用机理
2.1 模型设定与无约束均衡
2.1.1 基本假设
2.1.2 无约束下的均衡解
2.1.3 权重系数的简化与均衡分析
2.1.4 俱乐部的反应函数图像
2.2 硬工资帽政策对俱乐部投资决策的影响
2.2.1 当
$ \mathit{\alpha } \leqslant 0.5 $ 时硬工资帽政策的影响2.2.2 当
$ \mathit{\alpha } > 0.5 $ 时硬工资帽政策的影响2.3 软工资帽政策对俱乐部投资决策的影响
3. 研究结论、政策启示和未来展望
3.1 研究结论
3.2 对中国职业体育联盟的政策启示
3.2.1 进一步完善硬工资帽政策的制定与实施，审慎选择软工资帽政策
3.2.2 推进俱乐部股权多元化结构性改革，合理控制胜率最大化和利润最大化股东比例
3.2.3 有效把控工资帽政策规制力度，主动应对疫情冲击下的球员欠薪、球队破产等问题
3.3 研究不足与未来展望
