在体育管理心理研究领域存在许多具有理论和实践价值的抽象结构与潜在变量，例如市场需求、领导风格、组织文化、消费动机、体育场馆氛围、服务质量、教练绩效、运动员品牌形象、赛事遗产和体育赌博等等，它们构成了体育管理理论框架的基石。充分测量这些结构或变量是进行实证研究的基础，是体育管理成为独立学科的前提，基于此为体育管理提供的战略解决方案才是切实可行的。测量工具的结构对任何研究可能都是最重要的部分，即使是非常完美的研究设计也会因有缺陷的测量而失去价值，几乎所有社会、心理和行为研究中的理论概念都与不可直接观察的潜在结构变量紧密相关^[1]。基于此，本文拟对经典测量理论进行综述，讨论结构的定义及结构的来源，进而提出一个量表开发的五步框架。尽管量表开发的步骤和使用的统计技术都比较标准，但研究人员仍然需要注意每一步中隐藏的细微差别。本文对每个步骤及其效度进行了详细讨论，并在最后讨论了体育管理心理研究中的前沿和有争议的话题。

1.   经典测量理论综述

1.1   经典测量理论和真分数模型

测量理论起源于教育学和心理学，探讨普遍存在的测量问题和方法，相对于更现代的概化理论(generalizability theory)和项目反映理论(item response theory)，经典测量理论(classic testing theory, CTT)是20世纪初到60年代大量测量文献的一个集总，它为使用至今的能力、成就、人格和兴趣等的测量提供了理论基础^[2]。毫无疑问，经典测量理论在测量实践中应用最广，与更复杂的现代方法相比，经典测量理论的相对优势如下：①对小样本数据仍然有效；②数学公式相对直观；③统计包程序简单易用。一些学者甚至认为经典测量理论与项目反映理论之间几乎没有经验差异^[3]。经典测量理论的核心是真分数模型(true score model)，真分数模型的本质是任何观察到的测试分数都可以被视为真分数和随机误差这2个假设分量的复合，它可以表示为：

式中，X为观察分数，T为真分数，E为随机误差。观察分数是假设其取值服从某种概率分布的随机变量。通常观察不到方程右边的变量，假设方程右边有两个分量。从概念上讲，真分数是所测项目的完美度量，但在实际测量中，真分数不可能得到，通常认为它等于同样条件下多次测量结果的平价值。误差分数是由测量误差导致的与真分数的偏差。测量误差是测量不可靠的根源，其中一个主要原因是测量工具中的项目并非测量的同一个对象。为了强调随机误差，CTT做出如下3个假设：①误差平均数为零，则测量均值不会系统地偏离真分数；②测量误差遵循正态分布；③测量误差与真分数不相关。

真分数理论是一个简单却很强大的测量模型，该模型指出大多数测量具有误差分量，误差分量会削弱观察均值与真分数的相关性^[4]。因此，真分数理论在一定程度上为信度理论奠定了基础，即没有随机误差的测量是完全可靠的，同时没有真分数的测量是完全不可靠的。在数学上，真分数理论定义信度采用了信度指数和信度系数。信度指数是真分数的标准差与观察分数的标准差的比，表示为$ {\rho _{XT}} = \frac{{{\sigma _{{\rm{true}}\;{\rm{score}}}}}}{{{\sigma _{{\rm{observed}}\;{\rm{score}}}}}}$，它表明了真分数与重复测量所得到的观察分数的相关性。另一种选择是用信度系数来表示信度，信度系数是平行测量所得分数之间的相关系数。平行测量定义为每个受试者(或受访者)在两种测试中都具有相同的真分数，并且两种测试的误差方差相等。数学上，它是真分数方差与观察分数方差的比，表示为$\rho \left( {{x_1}, {x_2}} \right) = \frac{{{\sigma ^2}_{{\rm{true}}\;{\rm{score}}}}}{{{\sigma ^2}_{{\rm{observed}}\;{\rm{score}}}}}$，其中，x₁, x₂是2个平行测量中的观察分数，σ_{true score}²是受访者期望值的方差，σ_{observed score}²是真分数方差和误差方差的总和。信度指数和信度系数都是纯粹理论上的概念，研究人员永远无法实现真正的平行测量。因此，由于不能计算真分数的方差，信度也就无法计算。在实践中，信度只能通过实际测量分数来估计。

1.2   测量的评价标准

一个好的测量工具应该同时具有内容效度、效标关联效度、结构效度和信度。此外，它应该是灵敏的。

1.2.1   测量的效度

效度用于衡量测量特定指标时所具有的准确程度。美国心理学协会在1954年定义了4个方面的效度，包括内容效度(content validity)、结构效度(construct validity)、效标关联效度(criterion validity)；其中，效标关联效度包括同时效度(concurrent validity)和预测效度(Predictive Validity)^[5]。内容效度指的是所测内容与预定要测量的特质之间的一致性程度。内容效度需要从所有内容中选取相关的、有代表性的、清晰的测量内容进行抽样^{[1, 6]}。效标关联效度指测量结果与作为效标的另一组测量结果之间的一致性程度。同时效度指测量结果与同时间采集的效标之间的一致性程度。预测效度是指目前的测量结果与将来的效标之间的一致性程度。Trochim等^[6]认为内容效度和效标关联效度都为结构效度提供了部分证据。从这个角度来看，测量的最终目标是保证它的结构效度，结构效度是指实际测量结果与所要测量的理论结构和特质的一致性程度。

结构效度的检验通常通过构建一个多特质-多方法的矩阵, 并检验其中的聚合效度和区别效度来完成^{[5, 7]}。文献[5]提出结构效度检验应至少包含以下3个步骤：①根据理论建立一个结构模型; ②针对假设的结构模型提出具体的测量方法; ③实证检验测量数据与假设结构模型的匹配程度。目前，主流的商业和体育管理文献中都按照Fornell等^[8]提出的“平均方差提取值”(average variance extracted, AVE)作为检验结构效度的方法。表 1为常用效度测量类型的摘要列表。

表  1  常用效度测量类型的摘要列表

Table  1.  A summary list of commonly used measurement validity types

类型	效度类型	定义
内容 效度	表面效度	量表题目看起来好像是测量所要测的特质，由外 行对题目内容做出判断
	内容效度	量表题目对所要测量特质的代表性程度，由专家 对题目内容做出判断
效标关 联效度	同时效度	该测量与同时进行的标准测量之间的相关性
	预测效度	该测量能在多大程度上预测未来某个时间进行的 标准测量
结构 效度	聚合效度	测量同一结构的多重指标彼此间的高度相关性
	聚合效度	测量同一结构的多重指标彼此间的高度相关性
	区别效度	测量不同结构的多重指标彼此间的不相关性，常 与分歧效度互换使用
	分歧效度	定义为相关群组产生差异的能力[1]，常与区别 效度互换使用

下载: 导出CSV 

| 显示表格

1.2.2   测量的信度

信度是一个多维度的概念，指的是测验结果、因子或结构的可重复性、稳定性、一致性和精度。根据测量误差的来源，大致分为以下4种信度系数。①稳定系数(stability，跨时间的一致性)。稳定系数的主要测量方法是重测信度，即对同一组受试者以相同的测试方法在不同的时间进行测试, 所得结果的一致程度。②等值系数(equivalence，跨形式的一致性)。等值系数的主要测量方法是复本信度，即让同一组受试者进行内容范围相同但表达方式不同的测试, 所得结果的一致程度。③内在一致性系数(internal consistency，跨项目的一致性)。内部一致性系数的主要测量方法是克隆巴赫α系数，它可以被看作是所有折半相关系数的均值^[6]。其他内部一致性测量方法包括项目间平均相关系数、项目与总分间平均相关系数以及折半信度。④评分者信度(不同评分者测量的一致性)，即2个或2个以上评分者为同一个受试者进行重复测试, 所得结果的一致程度。可以通过计算不同评分者对特定问题集的选定比例或者打分结果的相关系数来测量。

在体育管理研究中，不是上述所有类型的信度都同等重要，研究者更加关注测量结果的稳定性和内部一致性，而内部一致性应从稳定性分析中分离出来^[1]。通常情况下，内部一致性系数值高于稳定性系数值^[9]。此外，在某些领域的研究中，评分者信度可能需要多个采访者、观察员或者测试管理员参与测试过程。表 2是常用的信度摘要列表。

表  2  常用的信度摘要列表

Table  2.  A summary list of commonly used reliability measures

维度	信度	摘要
稳定性	重测信度	用同一量具对同一组被试者测量2次，得出2次测试结果的相关系数
等值性	复本信度	对同一对象实施2个同一性质的测验，得出2个测验得分的相关系数
	折半信度	将测验分为两半，计算两半得分的相关系数
稳定性和等值性	平行信度	类似相关系数的概念定义，采用严格的平行测试，常与复本信度互换使用
	复本重测信度	对同一对象在不同时间实施2个同一性质的测验，得出两个测验得分的相关系数。它 通常被称为复本信度
内部一致性	项目间平均相关	同一维度内任意2个题项的相关系数的均值
	项目总分平均相关	同一维度内任意题项与该维度总分的相关系数的平均值
	克隆巴赫系数	数学上，等价于同一维度内所有可能的折半相关系数的均值
	库德-理查德森系数(K-R20)	类似于克隆巴赫系数，但只适用于只有2种选择记分的测量
	斯皮尔曼-布朗公式	内部一致性表示为题项数目与所有项目间的平均相关系数的函数
评分者信度	百分比一致性	易于计算和解释，但不能解决频数一致性和隐含一致性问题
	卡帕系数	考虑到可能出现的频数一致性问题，更稳健的方法是计算评分者的分类项得分
	Krippendorff’s Alpha	一种更复杂的检验方法，适用于3个或更多评分者的一致性检验

下载: 导出CSV 

| 显示表格

2.   体育管理心理量表开发的框架

在本节中，笔者基于经典测量理论^{[1-2, 5]}和相关领域的测量实践^[10-12]提出了一个量表开发的过程。围绕着结构的3个潜在来源进行相关内容的组织：①基于现有文献(类型一)；②基于特定研究背景(类型二)；③观察创造(类型三)。笔者尤其强调每一步如何与效度和信度检验相关联。

根据结构来源的不同，量表开发过程存在差异。严格地说，类型一的结构测量是对量表的验证而不是开发。首先，量表结构的定义和条目都来自于现有的文献。然后，利用验证性因子分析(CFA)对量表的心理特质进行检验。类型二的结构测量同时涉及演绎法和归纳法。通常，采用演绎法从文献中获取结构的定义和法则框架，结构的内容则基于现有理论和对一个或多个体育管理背景的观察进行归纳，最终的结构条目通常是演绎法和归纳法混合使用的结果。如果研究人员对量表的理论有足够的信心，量表心理特质检验可以直接使用CFA验证，然而处理这种类型量表更为恰当的方法是，首先采用探索性因子分析(EFA)，然后再采用验证性因子分析。类型三的结构测量涉及归纳法。这一类型量表中的条目通常是归纳法的结果，例如面试、小组讨论或直接观察。量表的心理特质检验几乎总是需要两个步骤。因子结构应首先使用EFA进行检验。使用独立样本的CFA是必要的后续步骤。类型三的真正挑战是提出一个可以检验的新量表的法则框架。类型三的结构测量要求对理论发展有重大的贡献。

2.1   步骤一：在法则网络(nomological network)中定义结构

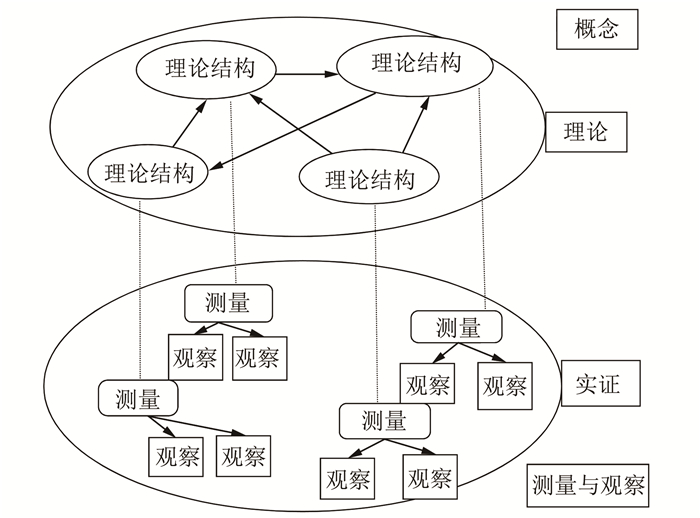
第1阶段是在理论背景下定义结构的准确概念。所有结构都来自于理论和实证域^[14]，第1步主要涉及结构的理论域，而第2步主要涉及结构的实证域。正如前面讨论过的，结构的数量可能没有限制，结构可以被随意命名。结构的验证只能在理论框架中进行。至关重要的是，研究者必须在量表开发的初始阶段就开始考虑结构效度的问题。图 1提出了一个假设的法则网络。

图  1  法则网络示意

Figure  1.  An illustration of nomological network

下载: 全尺寸图片 幻灯片

结构的理论定义由前人的理论并结合自身观察演变而来。关于类型一和类型二的结构，通常有大量文献提供研究者结构的定义和法则网络。对现有文献综述的全面阐述应该可以为量表开发提供足够信息。而类型三的结构，通常需要在开发量表之前进行某种定性研究，以揭示相关的理论基础。定性研究的目的是揭示结构的理论领域，并建立进一步研究的试验性的法则网络。

事先写一个简短而正式的结构描述是非常有用的。例如，基于对现有理论的回顾(即充分重要性模型、理性行为理论和计划行为理论)，将体育管理中的市场需求概念化为活动参与和再次参与驱动力的一个多维的态度结构^[13]，这个定义与传统经济学文献中的概念明显不同，市场需求与活动参与之间的预测关系是一个法则网络，其中市场需求是可以验证的。基于文献综述，Li等^[14]将赌博成瘾定义为一个广义的概念，既包括只有少量临床症状的问题状态，也包括具有更严重症状的病理状态。为了测量体育场景下的参与行为，Yoshida等^[15]将粉丝参与定义为“体育消费者在非交易市场中的额外行为，该行为使他或她最喜欢的运动队、团队管理层和其他球迷受益”。法则网络提供了粉丝参与量表的结构效度的佐证，包括粉丝参与的前因(团队识别、积极影响和荣耀关联)和粉丝参与的结果(购买意图和推荐意图)。

2.2   步骤二：定义内容域和初始条目池的生成

第2步是为结构的内容域提供一个实证定义，并且生成代表内容域的初始条目池。假定结构的实证域有其对应的理论域，共同实现对结构的操作化。它包括用于测量结构的特定观测变量的集合。理论域和实证域之间的匹配程度是检验结构效度的另一种方法。

2.2.1   层级问题

体育管理研究中结构测量的一个难题是，结构通常在不同的抽象层次或广度上有一个有序的层级结构^[16]。在体育管理中的二阶结构(second-order construct)是很常见的。这意味着主结构本身包含子结构，通常称其为维度或因子。例如，通常认为态度具有认知、情感和协同成分^[17]；因此，不仅需要定义一个态度的主结构，还要定义等其理论和实证上的子结构。本质上，这些子结构的实证定义为结构提供了内容域。而且，通常采用表示子结构的实证域来生成初始条目池，因此形成二阶结构。

以Byon等^[13]2010年的研究为例，市场需求的实证领域包括主队、客队、体育象征、经济考虑、运动推广和合理的进度安排。假设可以通过观察和测量这6个维度测量市场需求的结构。因此，市场需求是一个二阶结构，研究人员需要在理论和实证上定义6个维度。例如，“主队”在概念上被定义为“由主队表现、超级巨星的存在、主队球员的运动质量、胜败记录、主队声誉和主队的联赛积分排行位置等属性来表示主队的感知质量”。尽管研究人员没有明确指出，但这个结构的实证定义是消费者对团队属性的评分。应当注意，理论定义涉及“属性”，而实证定义涉及“消费者对属性的评分”，这是理论域与实证域之间的差异。基于实证定义，主队的内容域包括消费者对主队表现、超级巨星的存在、主队球员的运动质量、胜败纪录、主队声誉和主队的联赛积分排行位置等属性的评分。

2.2.2   内容域的抽样与效度

量表开发的一个重要任务是选择最能代表该内容域的条目。根据内容域的宽度(窄度)，通常不可能创建测量结构所有可能的条目。研究人员经常使用条目样本来表示这个定义域，这在检验理论中被称为域抽样。域抽样与统计中的采样的概念类似。在量表开发中，域抽样的全体是可以用来表示内容域的所有条目的集合，样本则是量表中的条目。条目对该内容域的代表性是先前讨论的内容效度的概念。因此，该步骤中的关键任务之一是确保内容效度。表 3是对一阶和二阶结构理论域、实证域以及量表条目的说明。

表  3  一阶和二阶结构的理论域、实证域和量表条目说明

Table  3.  An illustration of theoretical, empirical domains of first-order and second-order constructs and scale items

二阶结构	市场需求	粉丝参与
理论域	驱动运动参与和再次参与的多维态度结构	体育消费者在非交易市场的额外行为，使他或她最喜欢的运动 队、团队管理层和其他球迷受益
实证域	市场需求包括主队、客队、体育象征、经济考虑、运动推广和合 理进度安排	一个多维行为结构, 包括管理合作、亲社会行为和不良绩效 容忍
一阶结构	体育象征	不良绩效容忍
理论域	对专业运动队特点的整体感知	体育迷的持续行为在长时间内是稳定一致的，不受比赛价格、 运动员表现、运动队积分、运动员转到其他运动队等因素影响
实证域	体育迷对竞争的激烈程度、专业体育运动队的知名度、比赛时 长、高水平的技能、比赛中的最佳运动员和比赛速度的感知	体育迷自述其自身稳定性、比赛价格、运动员表现、运动队积 分、运动员转到其他运动队等因素对其产生的影响
量表条目	1.运动项目
	2.竞争的激烈性
	3.职业运动队的知名度	1.我穿着代表(球队名称)球迷的服装，即使球队的赛季不理想
	4.比赛的持续时间	2.我在我的衣服上显示(球队名称)的标志，即使该球队表现  不佳
	5.高水平的技能
	6.运动中的最佳球员	3.即使(球队名称)有不成功的赛季，我仍穿戴显示球队队名的  服装
	7.比赛速度
	8.职业运动队的体育能力	4.我穿着显示球队重要信息的衣服，即使(球队名称)打得不好
	9.高水平的竞技
	10.热爱职业运动队

下载: 导出CSV 

| 显示表格

2.2.3   条目库的形成

下一步是形成条目库，它代表了结构的实证域(即内容域)。理论上这个条目库应尽可能覆盖内容域的所有内容。在量表开发中，通常都以一个较大的条目库作为起点。对于第一类结构，通过详细的文献综述可以得到一个良好的条目库。文献综述需要阐明结构的定义、包含的维度以及测量的心理特质和条目。对于第二类结构，仅进行理论综述是不充分的，更恰当的方法是结合定性研究得到符合实际的条目。最常用的定性研究方法包括观察法、采访、小组讨论、头脑风暴等。为了开发量表测量市场对跆拳道学校的需求，KIM等^[18]从以下4个步骤着手建立了他们的初步模型：①文献综述；②跆拳道学校运作的现场观察；③采访跆拳道学校的校长、管理负责人和学校成员；④用德尔菲法检验内容效度。为了开发量表测量体育彩票领域中的赌博问题，Li等^[14]通过定性研究发展构建了赌博问题的评估模型，定性方法包括了文献综述、对中国体育彩票主管部门的采访、体育彩票零售地点的采访、顾客访问以及查看官方热线电话的服务记录。对于第3类结构，通常没有相关的文献作为参考，研究人员必须依赖定性研究产生所有的条目。文献[19]的研究提供了这一类型的例子，如通过定性研究形成一般条目库，为后继的量表开发奠定基础。

2.2.4   条目的组成

条目的书写也是条目库生成过程中一个重要的步骤。这里列举几条经验规则：第一，条目简洁，内容完整；第二，条目易于理解，阅读后不产生任何歧义，避免使用多重否定等容易带来疑惑的句子；第三，避免使用复义条目。复义条目是指一个条目有2种或多重含义。例如，“XXX健身中心是可靠的和响应的。”就是具有双重含义的句子。这个问题应该分成2个条目，即“XXX健身中心是可靠的。”和“XXX健身中心是响应的。”实际上，用“快速的”可能比“响应的”更好理解。有时候，复义问题的表达更为微妙。例如，“我认为我自己是UNM林狼篮球队的粉丝。”这句话是一个复义问题，因为这个学校既有男子篮球队也有女子篮球队，而且回答者也可能有不同的粉丝类型。因此，这个条目应该分解成2个条目。最后，条目的书写格式也决定了回复的格式。尽管有不同类型的量表和回复格式，利克特量表是体育管理文献中使用最多的。在实践中，比较常用的是五点或七点利克特量表，选择范围从强烈的不同意到强烈的同意。

2.3   步骤三：条目的精炼

初始条目库建立之后，第3步是对条目的校订和精炼。这个过程的目的是修改或删除“不好的”条目，这些条目对测量的效度和信度都没有贡献。通常，在这个步骤中可以采用两种处理方法。第1种方法是基于专家意见和先导性研究；第2种方法是基于统计指标，如克隆巴赫α、项目总分相关系数和因子载荷。值得注意的是，除非有足够大的样本量和具有代表性的样本，当基于统计指标来删除条目时必须小心谨慎。笔者首先介绍第1种精炼条目的方法——专家小组法，第2种方法在下一步中介绍。

2.3.1   专家小组法

专家小组法是经常使用的方法。一群拥有专业领域知识的专家被邀请对初始条目库进行审查。这个过程有多重目的，即同时实现量表内容效度和结构效度的优化。首先，专家可以通过评估结构和实证定义来评价条目的代表性和可操作性。例如，态度的结构定义为认知、情感和意图三者的结合，但是实证中却忽略了意图；或者态度定义为一阶结构的情感，但是实证中却错误地加入了认知的条目。领域专家(比如，熟悉态度理论的专家)会给予操作性的建议。第二，专家可以评估条目与结构的关联程度。通过向专家提供结构的实证定义，专家可以逐条评价条目与结构的相关性。最后，专家会评估每一个条目的清晰性和简洁性，尤其是那些对量表开发过程非常熟悉的专家的意见非常有价值。

2.3.2   先导性研究

专家小组法之后是先导性研究。先导性研究的目的是进一步测试条目语言的准确性、可靠性和有效性。条目语言的准确性可以基于被访问者对条目含义的理解来判断。研究者通过组织测试、与目标人群面谈等来帮助他们找到困惑或容易产生错误理解的条目。更正式的方法是使用一种称为认知报告的技术。认知报告能够反映回答者理解问卷或测量工具的意图，测量工具在文化背景和问题背景上都与目标人群高度相关^[20]，这一技术常用于通过翻译使用的量具。Mao等^[21]给出了这一技术在量表开发中应用的案例，该研究采用雪球式抽样和一对一谈话招募了10个学生，他们的教育水平从高中生到研究生。要求他们完成预先准备好的问卷，并记录他们回答每个条目时的速度和面部表情，以此判断条目理解的困难程度，并将此作为修正或删除条目的依据。

尽管做法不可取，但是很多研究者仍然采用小样本的方便抽样来进行先导性研究。样本量太小以至于缺乏进行评价量表心理特质的能力，例如进行因子分析。然而，一个先导性研究通常可以提供一个初步的量表评估。遵循经典的测量范式，对量表质量的首要要求是测试条目的相关性。有3个基本的统计指标可以用于先导性研究中，它们分别是条目总分相关系数、条目方差和条目均值。基于所有条目都是对第一级结构进行测量的假设，每一个条目都应该与量表总分相关。这个性质可以通过条目总分相关系数进行检验。

有2种条目总分相关系数的计算方法。未修正条目总分相关系数是计算单个条目与量表总分的相关系数；已修正条目总分相关系数也是计算单个条目与量表总分的相关系数，但量表总分不包含该条目自身的分数，可使用已修正的条目总分相关系数，因为未修正条目总分相关系数趋于夸大两者的相关性。此外，条目均值和方差也是评价条目心理特质测量的两个重要指标^[22]。在理想情况下，条目均值应该趋近于测量范围的中心，例如在一个5点量表中，条目均值的理想值是3。而条目方差应该相对较大，低方差表明所有的回答者给出了较为相似的答案，因此，该条目不具有区分能力。通常这些差异较小的条目会从量表中删除。值得注意的是，在采用小样本的方便抽样时删除条目时要格外小心谨慎。研究者需要考虑低方差问题可能是由小样本的同质性造成的，而不是条目本身的问题。如果在目标人群中抽取样本，并且方差有可能增加的情况下，研究者或许应该保留这些条目用于后续的研究。

基于初步分析的结果对条目进行修正。例如，研究者可能删除一些低方差的条目，或者修正一些条目总分相关系数较小的条目。如果已有条目的质量较差，有可能需要重新获得专家小组的意见或重新进行先导性研究；如果条目的质量尚可，研究者就可以进入正式研究阶段，对初始量表的条目在心理特质方面进行更加全面的探索，并进一步修正或精炼量表的条目。

2.4   步骤四：因子结构和心理特质

这一步的主要目的是评估新开发量表的心理特质。理想情况下，这一阶段研究的样本量应该足够大。需要较大的样本量有2个原因。第1个原因与学界对实验中采用大样本的争论有些相似。既然这一步的目标是评估条目的心理特质，那么关注点就应该集中在这些条目上。根据真分数模型，任何观察值都包含真分数和随机误差两部分，因此应该尽量减小误差的方差。理论上，足够大的样本量的随机误差趋于零，所以由参与者差异带来的随机误差可以忽略不计^[22], 为满足这一要求，样本量至少应该达到300^[23]。第2个原因是统计检验的要求，在这一步笔者采用的是统计方法，如EFA，要求使用大样本数据^[24]。就EFA而言，并没有“多大的样本量就足够大”这一问题的一致性答案，研究者们就这一问题给出了许多经验规则。Gorsuch^[25]建议即使变量的数量小于20，样本量也必须大于100。MacCallum等^[26]则认为如果条件允许研究者做EFA时应采样500以上的观察值, 建议样本量与变量的比例为20:1。需要注意的是，大样本并不同于具有代表性的样本，尽管大样本通常比小样本有更多的代表性。理想情况下，这一步应使用有代表性的样本。正如第三步中所述，研究者可能不恰当地删除了一些低方差的条目。有代表性的样本能更好地说明低方差是由条目设计的问题造成的，而不是样本同质性造成的。因此，使用有代表性的样本的因子结构和条目分析更可靠，并且所开发的最终量表的信度和效度更好，能更好地满足不变性假设。

这步关键的分析技术是EFA的应用，它在系列论文中被反复提及，这里不再重复。需要的读者可以参考介绍EFA技术细节的论文。EFA的目的是发现条目集合下隐藏的结构。通过前面三步，笔者提出了一个假设，就是已有的条目集合可以测量试图探讨的结构，而EFA被用来测试这个假设。假设结构是一维的，期望EFA得到一个因子，它能够解释观测数据的方差显著量。同时所有条目在这个因子上的载荷几乎都相等，即满足t检验的同质性假设。假设结构是多维的，笔者期望EFA得到多个因子。对于第1类结构，EFA并不是必要的，因为已经通过文献获得了对结构的洞见。对于第2类型结构，研究者通常有两条路可以走，由于笔者已经从文献中获得了对结构的洞见，因此可以跳过EFA直接进行CFA。这种做法可行的前提是对结构的假设非常成熟并且改动很小。否则，更理想的做法是先进行EFA，在进行CFA。第1条路中，CFA的作用是进行假设检验。如果结构通过CFA验证，则可以进一步进行结构方程模型(SEM)来测试结构的理论效度。与此相反，如果检验的结果发现得到的因子结构与假设的不一致，就需要修改理论，或者修改量表。EFA中使用相同的数据是必要的。对于第3类结构，在这步中EFA是必要的，用于揭示结构的构造。

2.5   步骤五：因子确认和理论效度

对量表的心理特质进行检验之后，下一步是利用CFA和SEM将理论法则网络中的核心结构与其他附属结构联接起来。理想情况下，笔者在这步中使用分离的样本数据，一个进行CFA，另一个进行SEM。样本量的大小和样本代表性的要求可能没有探索分析阶段那么严格。SEM需要的样本量由模型的复杂度和数据的正态性决定。绝大多数研究者建议样本量至少为200，或每个参数至少为5~10个案例^[27]。最近的两个仿真研究表明，小一点的样本量可能对SEM也是有效的，样本量可以在30(只有4个指标的CFA，载荷量在0.80左右)到450(中介变量模型)之间^[28]。Sideridis等^[29]的研究表明样本量为50~70就足够满足包含4个潜在变量的模型。尽管一个有代表性的样本是比较理想的，如果研究的目的只是确认因子结构和测试理论效度，那么这一要求完全可以放宽。Lynch^[30]认为，一个可能存在同质性问题的方便采样的样本在理论测试中是可以接受的。因此，当另一个样本的获得太困难或者成本太高时，将第四步中得到的较大样本分为2个子样本，一个用于EFA，另一个用于CFA和SEM是一种常用的做法。

笔者已经在之前的论文中介绍过了CFA，SEM将在下一篇论文中介绍，本文不再赘述。在这一步中还有一些工作要做。首先，需要进行针对核心量表的独立数据的CFA。笔者需要测试因子结构是否与EFA得到的一致，还需要测试因子载荷是否足够高(经验规则是大于0.70)。其次，SEM包含核心结构和测量结构，验证测量结构的效度需要在法则网络下测试量表的聚合效度和区分效度。在体育管理文献中，聚合效度和区分效度的检验是基于Fornell和Larcker (1981)提出的AVE进行的。AVE反映条目的有效方差与误差方差的相对大小，AVE的建议阈值是0.50^[8]。尽管大多数体育管理领域的学者主张AVE大于0.50，以表明量表具有聚合效度，但实际上AVE只是提供了关于条目聚合的信息，只是测量内部一致性的一种方法。相反，测量量表的聚合效度在体育管理文献中很少被提及和讨论，文献[7]指出聚合效度只能通过独立的方法进行验证，测量具有相同或相似结构的量表。2个独立方法得到的适度相关是量表聚合效度的明显证据。区别效度经常通过比较AVE的平方根和结构的相关系数来判断，其标准是一个结构的AVE平方根应该大于该结构与模型中任意其他结构的相关系数^[8]。

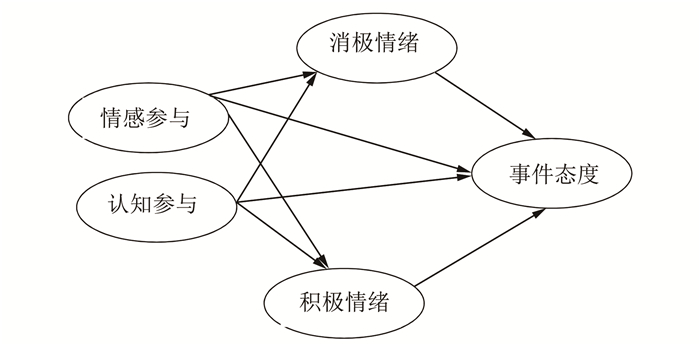
表 4是体育管理研究中报告量表聚合效度和区别效度的一个示例，图 2是与之对应的法则网络。对角线上是AVE的平方根。非对角线是结构间的相关系数。AVE可以通过对角线上数字的平方进行计算，并且所有的AVE都大于0.5，表明所有的条目都具有聚合效度(即内部一致性)。参与度、情绪和态度是通过不同方法测量的。其中，参与度通过7级语义差异量表测量，情绪通过4级利克特量表测量，态度通过5级利克特量表测量。数据的正相关和负相关与研究假设相符，并表明量表具有聚合效度。对角线上的数字都大于相关系数的绝对值，表明量表具有区分效度。

表  4  聚合效度和区别效度示例

Table  4.  An illustration of convergent validity and discriminant validity

	情感参与	认知参与	消极情绪	积极情绪	事件态度
情感参与	0.81
认知参与	0.625	0.78
消极情绪	-0.251	-0.203	0.73
积极情绪	0.281	0.177	-0.459	0.78
事件态度	0.607	0.568	-0.333	0.331	0.82
注:数据来源于Mao和Zhang 2013年一份未发表的研究报告

下载: 导出CSV 

| 显示表格

图  2  与表 4相对应的法则网络

Figure  2.  Nomological network corresponding to table 4

下载: 全尺寸图片 幻灯片

值得一提的是，量表的开发是一个迭代的过程。每个后续步骤的结果可能需要重新审视之前的步骤。同样，开发量表也不是一个研究的终点。量表的心理特质可能在以后的研究中被重新检验。只有表现良好的量表才会保留下来，并在未来的研究中被反复使用。

3.   结束语

基于经典测量方法，本文为量表开发的初学者提供了一个学习指南。基于结构的来源，本文给出了在不同情况下开发量表的可能框架：一个来自于其他相关领域的与研究背景无关的结构，可以直接用于自己研究中的测量，不需要开发新的量表，只需要进行验证就可以了。在体育管理心理研究中最常见的情形是，结构来自于其他相关学科，需要结合体育管理的背景进行适当修改，使用这一类结构时需要采用归纳的方法。根据研究者的先验信念，采用EFA进行研究。来源于体育管理领域直接开发的第3类结构是最少见的。开发这一类量表需要研究者具有很好的理论功底：一方面，结构的效度只能通过法则网络测试；另一方面，理论测试要求一个高质量的结构。理论测试和量表开发相辅相成。最后，必须指出的是，尽管经典测量理论占据主导地位，但它不是万能的，其他领域的研究者也提出了量表开发的其他可替代的方法，因此，研究者需要时刻保持谨慎和开放的态度。