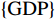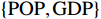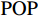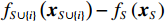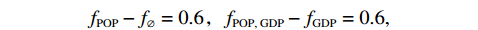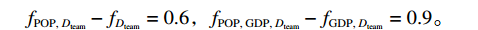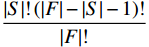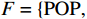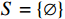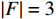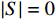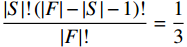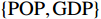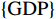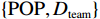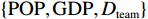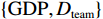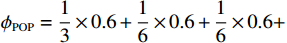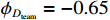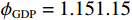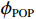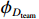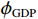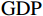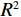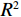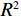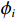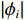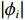Can Olympic Medals Be Predicted?Based on the Interpretable Machine Learning Perspective
-
摘要:
基于1992—2021年夏季奥运会的分项目成绩大数据,使用随机森林模型评估不同项目金牌和奖牌的可预测性,发现各项目存在较大的差异:对奖牌而言,可预测性最强的是乒乓球、羽毛球和游泳,而最弱的是水球、现代五项和排球。基于可解释机器学习方法挖掘社会经济因素对奥运奖牌的影响发现:①对同一个项目而言,女子项目的可预测准确性普遍高于男子项目;②代表队所在地区的人口规模、人均GDP、是否为主办国等因素对奖牌总数具有一定影响;③在特定项目上,代表队的传统优势(如中国的乒乓球、美国的田径等)对奖牌预测具有较大影响。
Abstract:Random forest models are constructed to predict the teams' medal numbers in different Olympic events based on a large data set of 1992-2021 Summer Olympic Games. It is found that apparent differences exist in the predictability of Olympic events. For the forecast of medals, the top three most predictable events are table tennis, badminton and swimming, while the bottom three are water polo, modern pentathlon and volleyball. With interpretable machine learning methods, the social-economic features are further investigated which have important effects on the performance of Olympic Games. The results show that: (1) For the same event, the prediction accuracy of women's events is usually higher than that of men's; (2) Factors like population, GDP per capita, and the game hosting have some influences on the medal numbers; (3) For specific Olympic events, some traditionally advantageous events like table tennis in China and athletics of the USA have a large impact on the medal forecast.
-
Keywords:
- Olympic medal /
- machine learning /
- feature importance /
- SHAP method /
- Shapley value
-
比赛结果的不确定性是竞技体育的魅力之一。然而,一些代表队在某些特定项目上的强大实力保证了其较高的获胜概率,从而使这些项目的胜负具有较高的可预测性。例如,在乒乓球男子团体项目上我国连续10次获得世界杯赛冠军,展现了我国在乒乓球项目上的强大实力。不同体育竞赛项目的表现在多大程度上可以被预测?哪些社会经济因素会影响各代表队在奥运会各项目上的表现?对于不同代表队在奥运会上的表现,已有研究主要关注代表队整体层面的奖牌分布,而未讨论其在不同项目上的差异。Bernard等[1]使用Logit模型分析奥运奖牌榜发现,一个奥运代表队所代表的国家或地区人口越多、人均国内生产总值越高、是该届奥运会的主办国,则该代表队获得的奥运奖牌数越多。Schlembach等[2]利用随机森林模型预测了各代表队在奥运会上的表现,评估了不同特征变量对预测的贡献。上述2篇文献关注的都是社会经济指标对一国或地区在奥运会上的总体表现,即金牌或奖牌总数,未探讨这些因素对不同项目影响的差异。事实上,不同代表队在不同项目上的表现存在较大差异。例如,美国作为体育强国,长期位于奥运奖牌榜首位,但在乒乓球、羽毛球等项目上美国运动员从未获得过奖牌,整体加总的数据无法解释这一差异。另外,从提高体育成绩的角度看,需要分项目讨论影响成绩的因素。因此,本文在评估不同项目可预测性的同时,也关注社会经济因素对不同项目影响的差异,填补该领域研究的空白。
具体而言,本文基于1992—2021年夏季奥运会代表队各项目成绩数据,利用随机森林模型预测各奥运代表队在各分项目上的表现,在此基础上比较不同奥运会项目表现可预测性的差异。在Schlembach等[2]的研究基础上,采用可解释机器学习的方法,即SHapley Additive exPlanations(SHAP)方法[3-4]对训练后的模型结果进行分析,讨论影响不同奥运项目成绩的社会经济因素。
1. 研究方法与模型构建
随着大数据收集和存储技术的不断进步以及机器学习新算法的涌现,人工智能技术作为专家决策的辅助手段之一,被越来越多地用于体育成绩的预测和竞技体育政策的制定。与传统的计量回归方法相比,机器学习方法具有更强的适应性和灵活性,能够更好地处理大量复杂数据,尤其善于分析数据中的非线性关系和高维问题。在体育相关预测中,现有的大多数研究[5-11]主要是利用机器学习方法分析运动员个体信息对运动员成绩的影响,尚无研究基于机器学习方法考察社会经济因素对代表队不同竞技项目表现的影响。
本文参考Schlembach等[2]的方法,选用随机森林作为分析的主要模型。随机森林由多个相互独立的学习器通过线性组合构成,能够在整体上降低预测偏差,具有较强的稳健性[12]。在社会科学实证分析中,随机森林方法得到了广泛的应用,例如,Athey等[13]、Wager等[14]将随机森林方法用于政策评估,李斌等[15]、陈小亮等[16]则发现在连续型经济和金融变量的预测中随机森林方法的表现尤为优异。本文在代表队—项目层面训练模型,然后预测代表队在分项目上获得的奖牌和金牌总数,在此基础上考察各代表队在分项目上表现的可预测性是否存在显著性差异。
除了可预测性结果,本文量化评估了各种社会经济因素对代表队不同项目的影响程度。众所周知,机器学习方法本身过于复杂,往往被视为一类“黑箱”方法,难以解释其背后的经济含义。因此,在对机器学习方法得到的结果进行解释时,通常需要借助额外的解释方法。常用的解释方法有部分相关图法、累积局部效应法以及和模型无关的局部可解释方法等[17]。但是,Lundberg等[3]研究表明,对于随机森林这类交互建模的方法而言,上述方法得到的变量权重在不同的评价体系之间可能会存在较大差异,甚至相互之间不具备比较的一致性。另外,随机森林模型自带的自变量重要性(feature importance)筛选方法在选取自变量时会更加偏好取值较多的离散型变量和连续型变量。鉴于上述方法都存在一定的缺陷,本文选用SHAP方法[4]作为可解释方法。
SHAP方法为一种全新的“模型无关的可加特征归因方法”(Model-Agnostic Additive Feature Attribution Methods)。该方法创造性地将博弈论中的Shapley值[具体定义见下文式 (2)]用于识别特征变量的重要性。Shapley值的概念来源于合作博弈理论,是一种基于贡献的收益分配方式,由2012年诺贝尔经济学奖得主罗伊德·沙普利提出。该方法分解出每个特征变量对模型预测所作的贡献,并用Shapley值度量贡献大小(或重要性),具有唯一性,且具有一系列良好的理论性质[4]。因此,本文通过Shapley值评估和比较不同特征变量的重要性(Shapley值越高,表示该特征变量对模型预测的贡献越大,与预测结果的相关性越强,越有可能是影响被预测变量的重要因素)。
本文使用的可解释方法提供了不同于传统计量方法的另一种视角。传统计量方法侧重于对变量的解释和统计推断,但机器学习方法往往比较复杂,重预测轻解释,缺少严格的大样本理论,从而不能进行严谨的统计推断。SHAP方法虽然仍不能为特征变量提供严格的统计推断,但通过Shapley值可对每个特征变量的重要性进行评估,并识别哪些特征变量在模型预测中相对重要。因此,与传统计量方法一样,SHAP方法也试图解释特征变量的作用。另外,与传统计量方法相比,机器学习方法不采用固定的参数化建模方法,更加适用于对复杂变量之间的相互作用和关系进行建模和预测,有利于更深入地理解非线性的现实世界。
本文采用的关键方法为可加性特征归因方法。该方法将每个特征变量对模型预测结果的贡献解释为“该变量(x)参与模型预测时对最后的预测结果(y)的贡献”。一个预测模型的“总预测贡献”可表示为:
$$g\left(\boldsymbol{x}\right)={\phi }_{0}+\sum\limits _{i=1}^{M}{\phi }_{i}\left(\boldsymbol{x}\right){\mathbb{1}}\left({x}_{i}\right) $$ (1) 其中:
$ \boldsymbol{x}=\left({x}_{1},\cdots ,{x}_{M}\right){'} $ 为M维的解释或特征变量,${\mathbb{1}}\left({x}_{i}\right)\in \left\{\mathrm{0,1}\right\}$ 是二值的指示变量,取1表示第i个特征变量用于预测,取0表示没有用于预测;$ g\left(\boldsymbol{x}\right) $ 表示最终预测结果,$ {\phi }_{0} $ 表示预测均值,$ {\phi }_{i}\left(\boldsymbol{x}\right) $ 表示特征变量$ {x}_{i} $ 对预测结果的边际贡献。测算$ {\phi }_{i}\left(\boldsymbol{x}\right) $ 的取值是可加性特征归因方法需要解决的关键问题。具体到本文的研究问题,$g\left(\boldsymbol{x}\right)={\phi }_{0}+\displaystyle \sum\limits _{i=1}^{M}{\phi }_{i}\left(\boldsymbol{x}\right)$ 表示“某一年份某代表队在某项目上所获奖/金牌数的对数值”,$ {\phi }_{0} $ 表示在该项目上所有代表队所获奖/金牌数的均值,$ {x}_{i} $ 表示第i个特征变量的取值,通过测算$ {\phi }_{i}\left(\boldsymbol{x}\right) $ 可以得到$ {x}_{i} $ 变化对所获奖/金牌数的影响,从而找到对预测奖牌变化作出较大贡献的特征。对于
$ {\phi }_{i}\left(\boldsymbol{x}\right) $ 的计算,SHAP方法借鉴了合作博弈理论中的Shapley值概念。SHAP方法将预测中所使用的特征变量$ \left({x}_{i}\right) $ 类比为合作博弈中的“参与者”,将模型预测结果$ g\left(\boldsymbol{x}\right) $ 类比为博弈结果的总收益。因此,评估变量$ {x}_{i} $ 对模型预测结果贡献度$ {\phi }_{i}\left(\boldsymbol{x}\right) $ 就相当于将收益在博弈参与人之间进行分配。特征变量$ {x}_{i} $ 的Shapley值为它对预测结果$ g\left(\boldsymbol{x}\right) $ 的贡献,其计算方法是将特征变量对模型预测结果的边际贡献进行加权求和,即$$ {\phi }_{i}\left(\boldsymbol{x}\right)=\sum\limits _{S\subseteq F\backslash \left\{i\right\}}\frac{\left|S\right|!\left(\left|F\right|-\left|S\right|-1\right)!}{\left|F\right|!}\left[{f}_{S\cup \left\{i\right\}}\left({\boldsymbol{x}}_{S\cup \left\{i\right\}}\right)-{f}_{S}\left({\boldsymbol{x}}_{S}\right)\right] $$ (2) 其中,i表示第i个自变量,
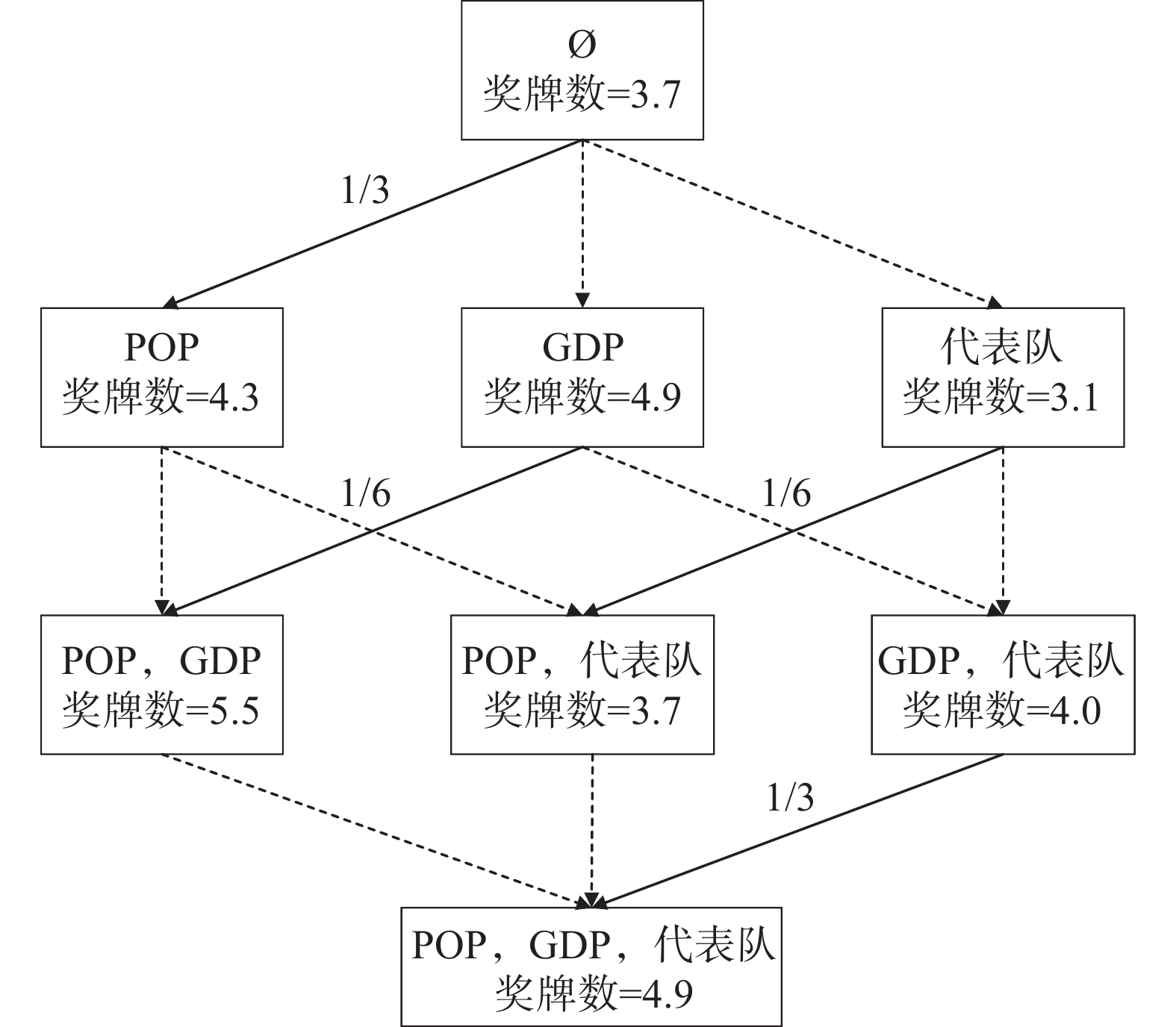
$ {\phi }_{i}\left(\boldsymbol{x}\right) $ 是其对模型预测结果的贡献度,F是模型所使用的特征变量集合,S是$ F\backslash \left\{i\right\} $ 的子集,$ {\boldsymbol{x}}_{S} $ 是S中包含的所有特征变量,$ {\boldsymbol{x}}_{S\cup \left\{i\right\}} $ 中包含了$ {\boldsymbol{x}}_{S} $ 和$ {x}_{i} $ ,$ {f}_{S\cup \left\{i\right\}} $ 和$ {f}_{S}\left({\boldsymbol{x}}_{S}\right) $ 分别是基于特征变量集合$ {\boldsymbol{x}}_{S\cup \left\{i\right\}} $ 和$ {\boldsymbol{x}}_{S} $ 训练不同模型得到的预测结果,$ \left|F\right| $ 和$ \left|S\right| $ 分别表示集合F和S中元素的个数。式(2)中的求和符号是对$ F\backslash \left\{i\right\} $ 中所有子集进行加总。图1展示了SHAP方法在本文应用的基本原理。假设特征变量集合
$ F=\left\{{\rm{POP}},{\rm{GDP}},{D}_{\rm{team}}\right\} $ ,其中,$ {\rm{POP}} $ 表示人口,$ {\rm{GDP}} $ 表示国内生产总值,$ {D}_{\rm{team}} $ 表示代表队虚拟变量。基于F预测该代表队在某项目上的最终奖牌数,并计算特征变量对测算最终奖牌数贡献的Shapley值。此时,S为$ F=\left\{{\rm{POP}},{\rm{GDP}},{D}_{\rm{team}}\right\} $ 的子集,f则是依托集合F的所有子集训练出的8个预测模型。特征变量人口($ {\rm{POP}} $ )的贡献可以通过在预测中是否包含$ {\rm{POP}} $ 信息所带来的最终奖牌数预测结果的变化量来度量。在图1中,当特征变量集为空集
$ \left\{\mathrm{\varnothing }\right\} $ 时,对最终奖牌数的预测结果为3.7,而特征变量集为$ \left\{{\rm{POP}}\right\} $ 时,对最终奖牌数的预测结果为4.3,在这一路径上新增人口信息对最终奖牌数预测结果的贡献为0.6。同样,当特征变量集为$ \left\{{\rm{GDP}}\right\} $ 时,对最终奖牌数的预测结果为4.9,而当特征变量集为$ \left\{{\rm{POP}},{\rm{GDP}}\right\} $ 时,对最终奖牌数的预测结果为5.5,在这一路径上新增人口信息对最终奖牌数预测结果的贡献为0.6。人口变量的综合影响可以通过对上述所有可能的路径进行加权求和得到。具体地,人口变量Shapley值的计算步骤如下:第1步,计算
$ {\rm{POP}} $ 对系统预测值的边际贡献,即式(2)中的$ {f}_{S\cup \left\{i\right\}}\left({\boldsymbol{x}}_{S\cup \left\{i\right\}}\right)-{f}_{S}\left({\boldsymbol{x}}_{S}\right) $ 。这在图1中体现为被4条实边连接的8个模型的最终预测值之差,具体包括:$$ {f}_{\rm{POP}}-{f}_{\mathrm{\varnothing }}=0.6 \text{,} {f}_{\rm{POP,\;GDP}}-{f}_{\rm{GDP}}=0.6 , $$ $$ {f}_{{\rm{POP}},\;{D}_{\rm{team}}}-{f}_{{D}_{\rm{team}}}=0.6 \text{,} {f}_{{\rm{POP}},\;{\rm{GDP}},\;{D}_{\rm{team}}}-{f}_{{\rm{GDP}},\;{D}_{\rm{team}}}=0.9 。$$ 第2步,根据公式
$ \dfrac{\left|S\right|!\left(\left|F\right|-\left|S\right|-1\right)!}{\left|F\right|!} $ 计算每个边际贡献的权重。以$ \left\{{\rm{POP}}\right\} $ vs$ \left\{\mathrm{\varnothing }\right\} $ 为例,$ F=\{{\rm{POP}}, {\rm{GDP}}, {D}_{\rm{team}}\} $ 、$ S=\left\{\mathrm{\varnothing }\right\} $ ,因此,$ \left|F\right|=3 $ ,$ \left|S\right|=0 $ ,所以$\dfrac{\left|S\right|!\left(\left|F\right|-\left|S\right|-1\right)!}{\left|F\right|!}= \dfrac{1}{3}$ 。同样,可以计算出剩下3个边际贡献($ \left\{{\rm{POP}},{\rm{GDP}}\right\} $ vs$ \left\{{\rm{GDP}}\right\} $ 、$ \left\{{\rm{POP}},{D}_{\rm{team}}\right\} $ vs$ \left\{{D}_{\rm{team}}\right\} $ 和$ \left\{{\rm{POP}},{\rm{GDP}},{D}_{\rm{team}}\right\} $ vs$ \left\{{\rm{GDP}},{D}_{\rm{team}}\right\} $ )的权重分别为$ \dfrac{1}{6} $ 、$ \dfrac{1}{6} $ 和$ \dfrac{1}{3} $ 。第3步,计算出
$ {\phi }_{\rm{POP}}=\dfrac{1}{3}\times 0.6+\dfrac{1}{6}\times 0.6+\dfrac{1}{6}\times 0.6+ \dfrac{1}{3}\times 0.9=0.7 $ 。类似地,可以计算出其他2个变量的贡献分别为
$ {\phi }_{{D}_{\rm{team}}}=-0.65 $ 和${\phi }_{{\rm{GDP}}}=1.151.15 $ 。可见,解释方法的可加性体现在最终预测值4.9等于无信息预测值3.7和3个变量贡献($ {\phi }_{\rm{POP}} $ 、$ {\phi }_{{D}_{\rm{team}}} $ 和$ {\phi }_{\rm{GDP}} $ )的加和。由于$ \left|{\phi }_{\rm{GDP}}\right|= 1.15 $ 对预测货币政策指数的贡献最大,可认为对预测该代表队在某项目上的最终奖牌数贡献最大的特征变量是$ {\rm{GDP}} $ ,接下来依次为$ {\rm{POP}} $ 和$ {D}_{\rm{team}} $ 。从上述计算过程可以看到,SHAP方法的另一个优点在于能够对预测进行分解,为每个数据样本的预测结果提供个性化解释。因此,对奥运会每个项目的预测都得到不同变量的Shapley值,可为精细化分析每个单项运动提供依据。将所有的样本预测分解得到Shapley值进行汇总,则可得到特征变量的Shapley值。Lundberg等[4]证明,SHAP方法比传统的变量重要性度量方法具有更好的性质,能够保证其结果在不同模型之间具有一致性。
2. 预测变量和数据来源
根据Bernard等[1]的方法,本文在随机森林模型中采用如下用于预测的特征变量:各国或地区人均GDP与世界人均GDP之比、人口占世界总人口的比重、是否为举办国、是否为上一届举办国、是否为下一届举办国、是否为社会主义政体、是否为计划经济体制。为了反映代表队在某个项目上的传统优势和潜在优势,本文还加入了代表队上一届在该项目上进入过前三名和前八名的数量这2个历史成绩变量;考虑到前面的2个历史成绩变量不能完全刻画国家或地区潜在特征的影响,如短期的成绩波动使得上届成绩并不能完全体现其优势,因此,还加入了代表队的哑变量。代表队的固定效应主要用来刻画国家或地区潜在特征对其奥运表现的长期影响。表1列出了奖牌总数预测所用到的特征变量。在对金牌数量进行预测时,还额外引入了该代表队在上一届奥运会获得的金牌数量。
表 1 预测所用的特征变量Table 1. Characteristic variables for prediction名称 定义 类型 GDPPC 人均GDP与世界人均GDP之比 连续变量 POP 人口占世界总人口的比重 连续变量 HOST 是否为举办国 0/1变量 LAST_HOST 是否为上一届举办国 0/1变量 NEXT_HOST 是否为下一届举办国 0/1变量 SOVIET 是否为社会主义政体 0/1变量 PLANNED 是否为计划经济体制 0/1变量 LAST_TOP8 上一届进入前八名的数量 连续变量 LAST_TOP3 上一届进入前三名的数量 连续变量 ISO 国家或地区哑变量 0/1变量 本文使用的奥运会代表队—项目层面的数据来自奥运会官方网站(https://olympics.com/en)。该网站包含了每个比赛项目中运动员代表的信息:运动员姓名、项目名称及名次、成绩记录和排名等。本文将原始数据进行了如下处理:①将国际奥委会(IOC)代表团队代码转换为ISO-3代码(国际标准化组织制定的国家地区国际标准代码),以使其在时间上保持一致。②处理了1992 —2021年代表队分裂和代表队合并的具体案例,也对相应的宏观经济变量进行了处理。③基于详细的“项目—运动员”数据,构建了“代表队—项目”层面的数据,包括金牌数、奖牌数、上一届进入前八名的数量等奥运成绩指标。在某些特殊情况下,如某些项目具有并列金银铜牌的情况,本文计算了每届奥运会每个项目的实际金牌总数和奖牌数。④根据项目特征对比赛进行分类。本文根据性别将项目分为男、女和男女混合项目。在每个类别下分别进行奖牌和金牌预测,以研究性别差异是否对各种特征的比赛项目产生不同的影响。
该数据集包含了1992、1996、2000、2004、2008、2012、2016和2020年(推迟到2021年举行)的夏季奥运会数据。统计数据囊括了最少派出1名运动员参加该届奥运会的代表队。对于个别代表队也进行了特殊区分。例如,1992年,独联体代表队(由来自俄罗斯、白俄罗斯等国的运动员组成)参加了夏季奥运会,将这些国家的宏观数据进行了对应的加总处理。
本文所使用的宏观经济变量(人口和人均实际GDP数据)的主要来源是世界银行。对于世界银行数据库中缺失的数据,利用Penn World Table和Maddison项目的数据进行填补。根据奥运会网站上的信息建立了代表东道国的虚拟变量。对于计划经济虚拟变量的定义,本文沿用Bernard等[1]的做法。
对奥运会项目数据做了如下处理。①以2020年东京奥运会的项目设置为标准,对历史上有过变动的项目进行了处理。②去除了2020年东京奥运会新增的5个项目(滑板、冲浪、攀岩、棒垒球和空手道)。③去除了高尔夫球、橄榄球和棒球3个项目。高尔夫球和橄榄球于2016年加入奥运会,可用的训练数据较少;棒球曾在2012年和2016年奥运会中被取消,2020年重新加入奥运会,数据间断。④在训练数据的选取中,只选用进入过前八名的代表队的比赛记录,排除未进入前八名的比赛记录对奖牌预测结果的干扰。经过上述处理后,本文得到了1992—2020年8届奥运会29个大类项目的18713条比赛记录。在对奖牌结果做模型拟合时,参照Schlembach等[2]的方法,对奖牌数加1后取自然对数。
3. 实证结果与分析
在随机森林模型中运用SHAP方法对影响最终奖/金牌数的预测变量进行识别。具体识别过程如下:①利用前文中描述的数据信息,使用随机森林模型对奖/金牌数进行分项目预测训练,训练集为1992—2016年夏季奥运会数据,测试集为2020年东京奥运会数据。②对每个项目的奖/金牌数预测分别构建随机森林模型。具体而言,在模型训练时的超参数选择上,将子树的数目设定为1000,使用均方误差来衡量分裂质量,将最大解释变量个数设定为总解释变量个数的1/3。③使用SHAP方法对模型训练结果进行分析,识别出各项目中与预测奖/金牌数关系最为密切的特征变量。
3.1 不同项目可预测性的差异
利用前述模型对2020年东京奥运会不同项目每个代表队的奖牌数和金牌数进行预测。基于预测结果和真实值之间的对比,评估在不同项目上模型预测的准确程度。笔者发现,虽然竞技体育普遍具有高度的不确定性,但不同项目的不确定程度存在非常大的差异。每个项目参与代表队的多少、各代表队实力的分布以及项目本身的偶然性都会影响奥运会项目的可预测性。
主要通过样本外预测表现评估不同项目的可预测性。样本外预测是在训练数据集之外的测试数据集上评估模型表现的一种方法,能直接反映模型在新数据上的表现, 但往往需要足量且能分出独立测试集的场景。笔者主要关注对2020年东京奥运会的预测,并对样本进行了固定的分割:1992—2016年数据作为训练样本,2020年东京奥运会数据作为测试样本。因此,该结构适合进行样本外预测评估。另外,未采用机器学习中最常用的交叉验证来评估模型,原因在于该方法适用于数据量较少或需更细致评估模型稳定性的场景,同时交叉验证对样本的随机分割并不适用本文的数据。因此,主要采用固定样本分割的样本外预测
$ {R}^{2} $ (可决系数)作为预测得分评估不同项目的可预测性,分数越高,代表可预测性越强,项目的不确定性越低。当然,也可采取其他评估标准,如预测的均方误差等。但与其他标准相比,样本外预测$ {R}^{2} $ 的一个优点是该测度不受测量单位的影响,易在不同项目之间进行可预测性比较。表2为2020年东京奥运会奖/金牌数样本外预测
$ {R}^{2} $ 排在前十和倒数前十的项目以及得分。从表2的左半部分可以看到,奖牌可预测性强(排前十)的项目分别是乒乓球、羽毛球、游泳、跳水、马术、击剑、柔道、自行车、摔跤、帆船,金牌可预测性强(排前十)的项目分别是花样游泳、跳水、乒乓球、射箭、马术、摔跤、游泳、篮球、水球、帆船。从表2的右半部分可知,奖牌可预测性最弱的10项是水球、现代五项、排球、网球、曲棍球、举重、铁人三项、篮球、跆拳道、射击,金牌可预测性最弱的10项是跆拳道、网球、足球、现代五项、排球、皮划艇、赛艇、铁人三项、射击、手球。表 2 2020年东京奥运会奖/金牌数预测得分前十和后十的项目Table 2. Top 10 and Bottom 10 predictable events in Tokyo Olympic awards/gold medal forecast预测得分前十 预测得分后十 奖牌项目 得分 金牌项目 得分 奖牌项目 得分 金牌项目 得分 乒乓球 0.8453 花样游泳 0.9707 水球 −0.0226 跆拳道 −0.5780 羽毛球 0.8424 跳水 0.9082 现代五项 0.0582 网球 −0.3175 游泳 0.8339 乒乓球 0.8197 排球 0.1018 足球 −0.2599 跳水 0.8314 射箭 0.7868 网球 0.1664 现代五项 −0.1613 马术 0.7932 马术 0.6956 曲棍球 0.2307 排球 −0.1437 击剑 0.7139 摔跤 0.6809 举重 0.2494 皮划艇 −0.0767 柔道 0.7108 游泳 0.6540 铁人三项 0.2954 赛艇 0.1077 自行车 0.7058 篮球 0.6335 篮球 0.3001 铁人三项 0.1536 摔跤 0.6684 水球 0.6325 跆拳道 0.3921 射击 0.1892 帆船 0.6528 帆船 0.6253 射击 0.4967 手球 0.2301 项目的可预测性强主要是因为有一个或少数几个代表队在该项目中具有超强实力。例如:中国在乒乓球项目上强大的综合实力导致奖牌的可预测性较强;而在花样游泳项目上,俄罗斯队在双人赛和团体赛上连续6届蝉联冠军,花样游泳项目金牌的可预测性最强。项目的可预测性弱主要是因为参与该项目的代表队众多,同时实力较为接近,导致竞争激烈。例如,在足球项目上有19个代表队都曾获得金牌或奖牌。同时,奖牌的可预测性和金牌的可预测性也存在差异。例如,在金牌的可预测性上篮球位居第八,在奖牌的可预测性上则位于倒数第八,这主要是因为历史上曾经有16个代表队获得奖牌,但只有4个代表队(美国、独联体、阿根廷和拉脱维亚)夺得金牌。同时,在篮球项目产生的18枚金牌中,独联体、阿根廷、拉脱维亚各自只获得1枚金牌,其余15枚金牌都为美国队所得。此外,一些项目(如射击)在比赛时运动员发挥的或然性较高,其金牌和奖牌的可预测性都位居后十。
3.2 各变量对不同项目预测结果的贡献程度
以奥运会足球、篮球、排球三大球项目为例,展示使用SHAP方法计算的各变量重要性的排序。首先对于每个样本观测,计算出每个变量的Shapley值(
$ {\phi }_{i} $ ),然后对整个样本关于Shapley值的绝对值进行平均,作为在整个样本上的贡献。列出使用$ \left|{\phi }_{i}\right| $ 均值度量的重要性影响前十的变量(表3)。值得注意的是,表3展示的是$ \left|{\phi }_{i}\right| $ 的平均值,而国家和地区哑变量的Shapley值具有稀疏性特征,即只是少数不为零,因此数值较小。表 3 对三大球项目影响前十的变量Table 3. Top 10 important variables in three major ball events forecast足球 篮球 排球 变量 Shapley值 变量 Shapley值 变量 Shapley值 POP 0.0491 LAST_TOP3 0.0463 LAST_TOP8 0.0586 GDPPC 0.0157 LAST_TOP8 0.0298 POP 0.0426 德国 0.0116 GDPPC 0.0163 LAST_TOP3 0.0410 LAST_TOP8 0.0101 美国 0.0155 GDPPC 0.0134 阿根廷 0.0085 POP 0.0154 巴西 0.0123 巴西 0.0083 澳大利亚 0.0086 意大利 0.0105 美国 0.0050 法国 0.0082 美国 0.0062 加拿大 0.0050 西班牙 0.0077 PLANNED 0.0043 LAST_TOP3 0.0043 塞尔维亚 0.0070 德国 0.0042 尼日利亚 0.0036 阿根廷 0.0051 HOST 0.0040 从表3可知,在三大球奖牌预测中,历史成绩变量(LAST_TOP3,LAST_TOP8)都是排名前十的解释变量,说明传统优势地位对奥运表现有着较大的影响。除了历史成绩变量,公认强队的哑变量基本都出现在重要性前十的因素中。例如,足球为德国、阿根廷、巴西等队,篮球为美国、法国、西班牙等队,排球为巴西、意大利、美国等队。这意味着国家或地区固定效应是历史成绩变量的有益补充,可以捕获潜在特征的影响。最后,人口(POP)和人均GDP(GDPPC)是影响这些比赛项目表现的主要因素。
3.3 国家(地区)潜在特征对奖牌预测的影响
特定代表队在特定项目上具有一定的传统优势,如体操项目中的中国队、美国队,足球项目中的巴西队、法国队。但该如何量化这种传统优势呢?①历史成绩变量在很大程度上可以刻画代表队的传统特征,因此,在预测变量中加入了上一届在该项目上是否进入过前三和是否进入过前八这2个变量。②加入了代表队哑变量,引入固定效应进一步揭示代表队潜在特征对其奥运表现的影响。如果2个历史成绩变量已经完全刻画了代表队的潜在特征,那么国家或地区固定效应对预测的贡献应趋于零。考虑了人口规模、人均GDP、东道主优势和历史成绩之后,通过SHAP方法计算代表队固定效应对最终预测的影响程度,即代表队Shapley值,并且列举了代表队固定效应对最终结果影响较大的一些代表队—项目的组合,分析在具体项目上代表队因素对结果的影响。表4列出了代表队固定效应对最后项目结果预测影响超过0.3的代表队和项目的组合。从表4可以看到,在上榜的代表队里,以欧洲代表队和苏联解体后的代表队居多,苏联解体后的代表队在擅长的项目上也较为集中,如摔跤、举重、拳击、体操等。
表 4 代表队固定效应对全样本奖牌预测值影响超过0.3的代表队和项目Table 4. Teams and events with Shapley value greater than 0.3 for team fixed effect (full sample medals prediction)项目 代表队 Shapley值 项目 代表队 Shapley值 射箭 韩国 0.4056 网球 捷克 0.3186 现代五项 俄罗斯 0.3083 俄罗斯 0.3019 帆船 英国 0.3557 田径 俄罗斯 0.4893 自行车 英国 0.3348 美国 0.4429 马术 德国 0.3035 白俄罗斯 0.3155 乒乓球 中国 0.3114 体操 俄罗斯 0.6031 跆拳道 韩国 0.3982 乌克兰 0.5039 柔道 乌兹别克斯坦 0.3624 白俄罗斯 0.3733 格鲁吉亚 0.3184 举重 哈萨克斯坦 0.4060 射击 俄罗斯 0.5194 格鲁吉亚 0.3601 斯洛伐克 0.3050 俄罗斯 0.3533 游泳 俄罗斯 0.5370 摔跤 俄罗斯 0.6216 美国 0.4977 白俄罗斯 0.3951 皮划艇 捷克 0.3718 哈萨克斯坦 0.3220 德国 0.3137 乌克兰 0.3173 跳水 中国 0.3324 拳击 俄罗斯 0.5723 俄罗斯 0.3051 哈萨克斯坦 0.5722 击剑 俄罗斯 0.5267 阿塞拜疆 0.3245 意大利 0.3147 乌克兰 0.3236 乌兹别克斯坦 0.3044 表5展示了在对金牌预测的解释中代表队固定效应影响超过0.3的代表队和项目组合,如中国—跳水、俄罗斯—体操、韩国—跆拳道等。表5中的项目—代表队组合数目明显少于表4,表明虽然某些代表队在某些项目上拥有强大的实力,但获得金牌的难度远远大于获得奖牌的难度。
表 5 代表队固定效应对全样本金牌预测值影响超过0.3的代表队和项目Table 5. Teams and events with Shapley value greater than 0.3 for team fixed effect (full sample gold medal prediction)项目 代表队 Shapley值 项目 代表队 Shapley值 田径 俄罗斯 0.3454 花样游泳 俄罗斯 0.3820 击剑 俄罗斯 0.4430 游泳 俄罗斯 0.3663 摔跤 俄罗斯 0.5997 美国 0.3484 跳水 中国 0.5192 举重 中国 0.4188 帆船 巴西 0.3144 伊朗 0.4031 网球 美国 0.3698 体操 俄罗斯 0.3826 跆拳道 韩国 0.6042 乌克兰 0.3424 3.4 不同性别项目预测结果分析
在2020年东京奥运会上,有146个男子项目、137个女子项目和15个男女混合项目。从奥运项目表现看,我国女运动员取得的成绩好于男运动员。在2020年东京奥运会中国代表团所获的38枚金牌中,女子项目22枚金牌,男子项目13枚金牌,混合项目3枚金牌。
利用分性别的项目比赛数据对男女项目分别进行了预测,识别在不同性别领域中男女项目各自的强项和代表队固定效应。区分了男女项目后,将数据分为2类重新训练了模型。从表6的左半部分可知,因为可供训练的数据集减少了一半,各项目在得分情况上相较于全样本模型来说都有较大程度的下降,但在男子乒乓球、男子跳水、女子田径等项目上,模型还是维持了相对较高的得分。此外,男子项目与女子项目的差异也说明一个代表队在一个项目上的实力是性别非对称的。
表 6 分性别奖牌数和金牌数预测得分前十的项目Table 6. Top 10 predictable events for medals and gold medals (by gender)奖牌项目 金牌项目 男子项目 得分 女子项目 得分 男子项目 得分 女子项目 得分 乒乓球 0.8601 曲棍球 0.7363 跳水 0.8926 跳水 0.9973 跳水 0.7914 跳水 0.6869 乒乓球 0.8909 花样游泳 0.9707 柔道 0.7011 田径 0.6729 帆船 0.7705 射箭 0.9693 摔跤 0.6957 足球 0.6664 水球 0.6054 水球 0.9339 赛艇 0.5854 游泳 0.6516 拳击 0.5598 乒乓球 0.9087 游泳 0.5748 体操 0.6439 摔跤 0.5494 篮球 0.8466 自行车 0.5739 花样游泳 0.6085 游泳 0.5196 自行车 0.5599 击剑 0.5350 手球 0.6062 柔道 0.4733 摔跤 0.5540 拳击 0.5273 乒乓球 0.5952 篮球 0.4298 柔道 0.5212 帆船 0.4885 皮划艇 0.5704 射箭 0.3715 游泳 0.4106 根据表6的右半部分可知,虽然在之前男女项目奖牌的预测得分因为数据量的减半导致模型拟合能力下降,但在金牌的预测上有几个项目的样本外预测得分较高。原因在于:①这些项目都各自存在传统的“超级强国”,在这些项目的表现上有着绝对实力。②一个代表队的某种性别在一个项目上的强势并不意味着另一个性别擅长此项目。将男女项目分开训练后,反而排除了另一种性别对模型预测能力的干扰。例如,韩国女子射箭队实力突出,排除了男子项目数据后,更容易预测女子射箭的金牌数。③不同于奖牌数,金牌需要预测的结果少,较少的预测数更容易让结果收敛,能够体现出该项目传统优势强国的作用,排除了银牌、铜牌数对结果的干扰。
在总的得分前十的项目中,从预测结果看,女子项目的模型预测质量远高于男子项目,在女子入围的6个项目中,有5个得分超过了90%,其中有3个超过了95%。这也从侧面印证了男子项目的竞争性要强于女子项目,其结果的不可预测性更强。由于男子项目的高水平运动员更多、更分散,对男子项目的金牌预测更加困难。这可能源于男女在竞技体育参与意愿、比赛激烈程度、赞助商数量、大赛奖金数量和受欢迎程度等多方面的差异。
表7展示了代表队固定效应对男子、女子奖牌预测值的影响超过0.3的项目—代表队组合。对比之前全样本的预测结果,在对性别分组后,代表队固定效应对各项目预测值的影响大多显著增加。同时,女子项目中发达经济体代表队的比重较高。平均而言,在发达经济体中女性地位较高,女性在这些代表队中可以获得更多的资源和受到较少的职业发展歧视,更有可能成为奥运会运动员。
表 7 代表队固定效应对分性别项目奖牌预测值影响超过0.3的代表队和项目Table 7. Teams and events with Shapley value greater than 0.3 for team fixed effect (medals prediction by gender)性别 项目 代表队 Shapley值 性别 项目 代表队 Shapley值 男子 射箭 韩国 0.4141 女子 射箭 韩国 0.5035 田径 美国 0.5389 现代五项 英国 0.3027 帆船 英国 0.4546 游泳 美国 0.3843 乒乓球 中国 0.3503 皮划艇 匈牙利 0.3606 跆拳道 韩国 0.4352 跳水 中国 0.3328 自行车 英国 0.3418 击剑 意大利 0.3274 击剑 俄罗斯 0.4623 举重 泰国 0.3340 体操 俄罗斯 0.3672 田径 俄罗斯 0.5335 现代五项 俄罗斯 0.3249 肯尼亚 0.3431 射击 意大利 0.3668 摔跤 日本 0.3199 俄罗斯 0.3249 射击 俄罗斯 0.4702 游泳 俄罗斯 0.4860 乌克兰 0.3351 美国 0.4213 德国 0.3223 柔道 乌兹别克斯坦 0.3972 体操 俄罗斯 0.4419 日本 0.3441 美国 0.3639 格鲁吉亚 0.3297 乌克兰 0.3339 皮划艇 捷克 0.3889 网球 捷克 0.3112 斯洛伐克 0.3245 俄罗斯 0.3070 举重 哈萨克斯坦 0.4568 俄罗斯 0.4080 格鲁吉亚 0.3291 伊朗 0.3220 拳击 哈萨克斯坦 0.5482 俄罗斯 0.5266 乌克兰 0.3746 乌兹别克斯坦 0.3282 阿塞拜疆 0.3244 摔跤 俄罗斯 0.6487 白俄罗斯 0.4472 乌克兰 0.3544 格鲁吉亚 0.3219 哈萨克斯坦 0.3013 表8呈现了在金牌数预测中,男女项目代表队固定效应对预测值的影响超过0.3的项目—代表队组合。男子项目代表队固定效应依旧分散,在有些项目上有2个代表队入围,而女子项目中单个代表队居多,这是男子项目的竞争更激烈所致。
表 8 代表队固定效应对分性别项目金牌预测值影响超过0.3的代表队和项目Table 8. Teams and events with Shapley value greater than 0.3 for team fixed effect (gold medals prediction by gender)性别 项目 代表队 Shapley值 性别 项目 代表队 Shapley值 男子 拳击 俄罗斯 0.3046 女子 射箭 韩国 0.3349 跳水 中国 0.3611 田径 俄罗斯 0.4171 跆拳道 韩国 0.3514 跳水 中国 0.3691 举重 伊朗 0.3816 游泳 美国 0.3555 游泳 美国 0.3013 花样游泳 俄罗斯 0.3820 乒乓球 中国 0.3402 跆拳道 韩国 0.4079 摔跤 俄罗斯 0.6951 举重 中国 0.3996 帆船 英国 0.3229 摔跤 日本 0.3182 澳大利亚 0.3184 击剑 俄罗斯 0.3410 意大利 0.3046 3.5 经济发展水平与奥运项目表现
Bernard等[1]指出,一个国家人口数量越多,人均GDP越高,该国获得的奥运奖牌越多。培养高水平运动员既需要有运动员的才华作为“种子”,也需要一国人均经济收入达到一定程度作为培养的“土壤”。不同于Bernard等[1]基于奥运总体奖牌的发现,根据分项目数据分段计算出人均GDP对应的Shapley值的均值后,识别出在特定项目上的人均GDP对项目结果影响的门槛效应。类似于不同收入阶层的后代在职业选择上会有明显的差异,发现不同经济发展水平的代表队在参与奥运项目的选择上也存在着明显差异。这主要是因为不同项目对经济发展水平的要求不同。
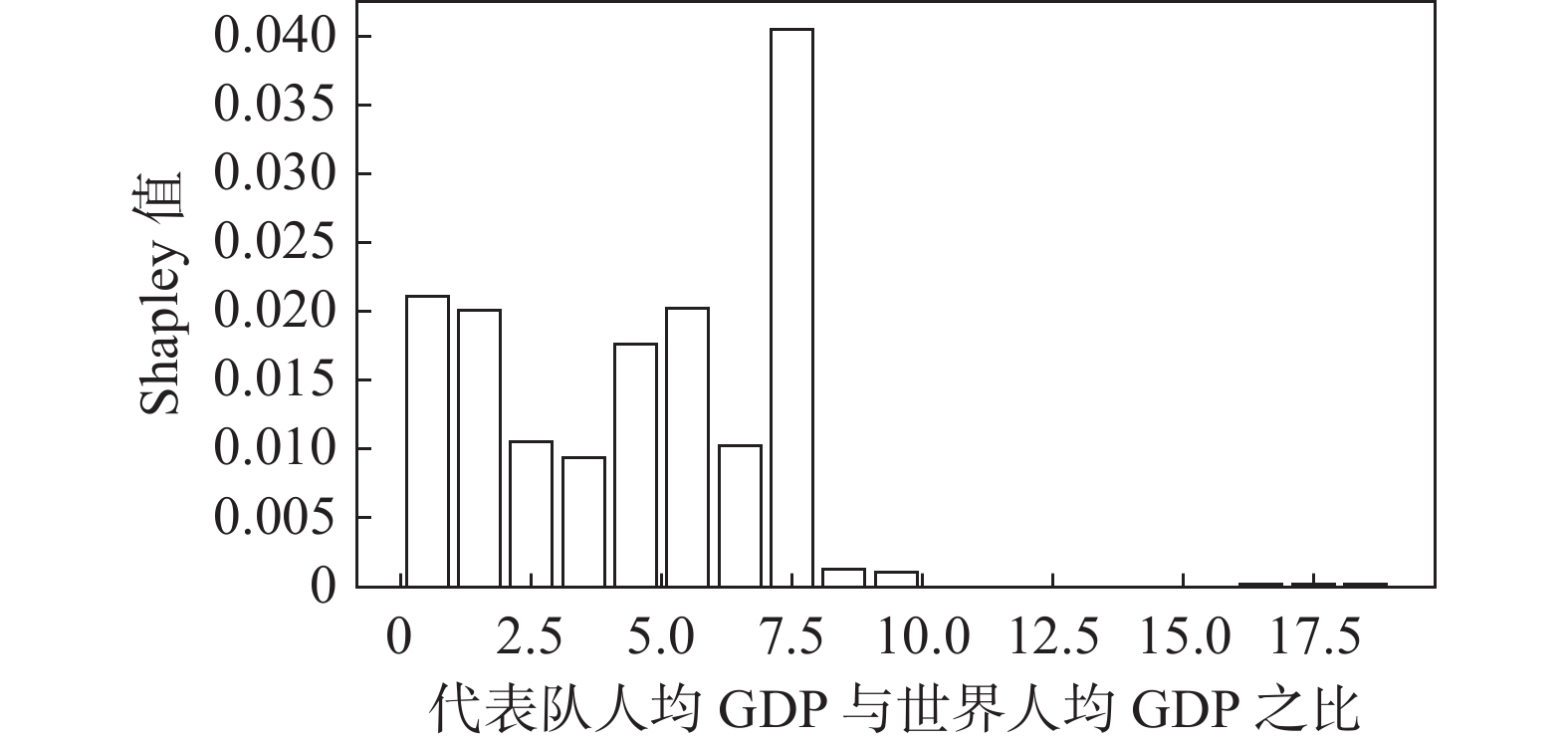
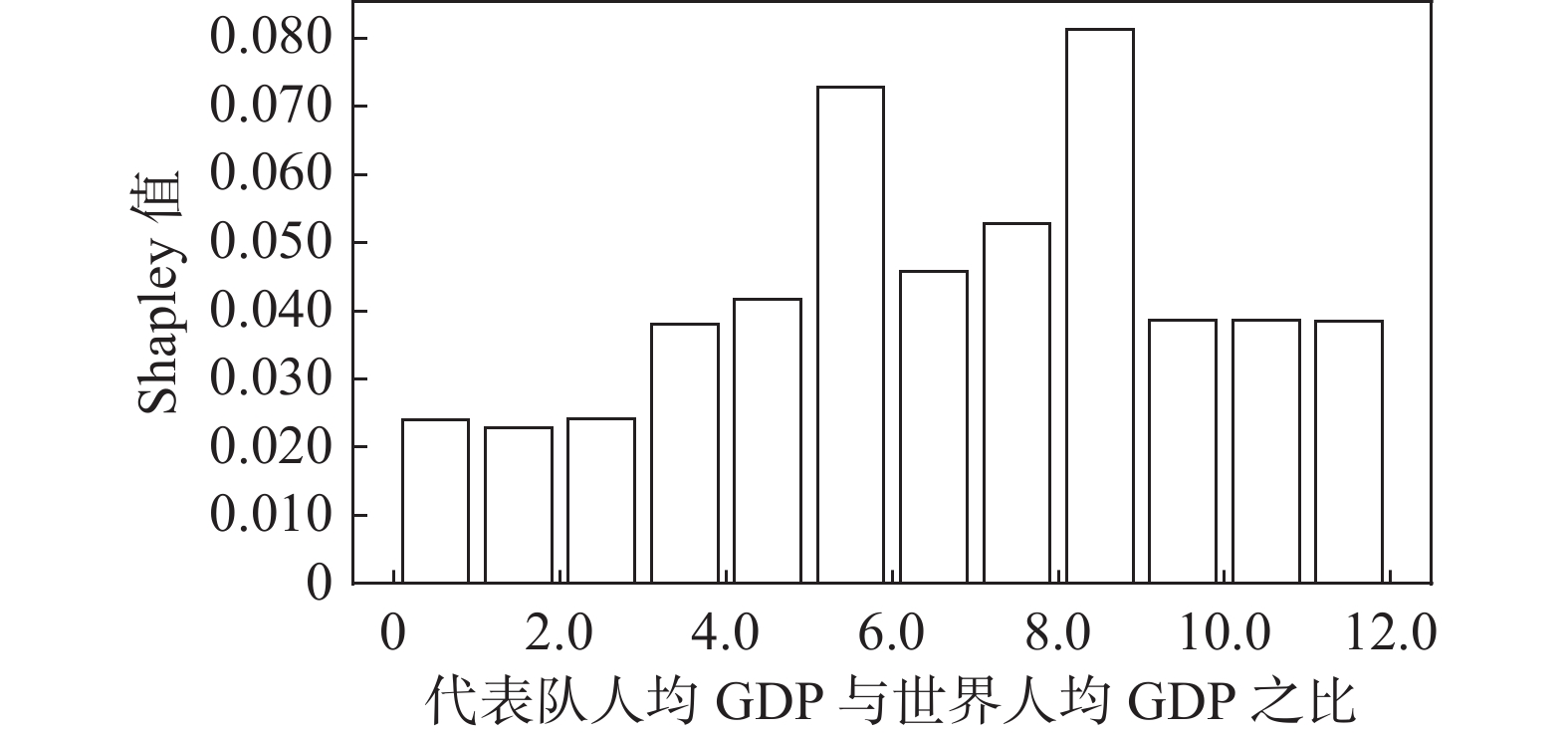
(1)一些项目(如举重)的参与代表队和奖牌获得者集中在发展中国家或地区。图2展示的是举重项目中人均收入因素(代表队人均GDP与世界人均GDP之比)及其对Shapley值影响的分布关系。将代表队人均GDP与世界人均GDP之比按整数倍分段后,计算出每一段内GDP因素对应的Shapley值绝对值的均值,代表了在该阶段上GDP因素对最终预测结果的平均影响,并将对应关系以直方图的形式展示。从图2可见,在举重项目上,参与代表队较多地集中在人均收入较低的国家或地区。
(2)对于一些项目(如马术)而言,强大的经济实力至关重要。如图3所示,马术项目的参与代表队大多出现在人均GDP是世界人均GDP 5倍以上的国家或地区,人均收入较低的国家或地区对马术项目奖牌的预测作用很小。
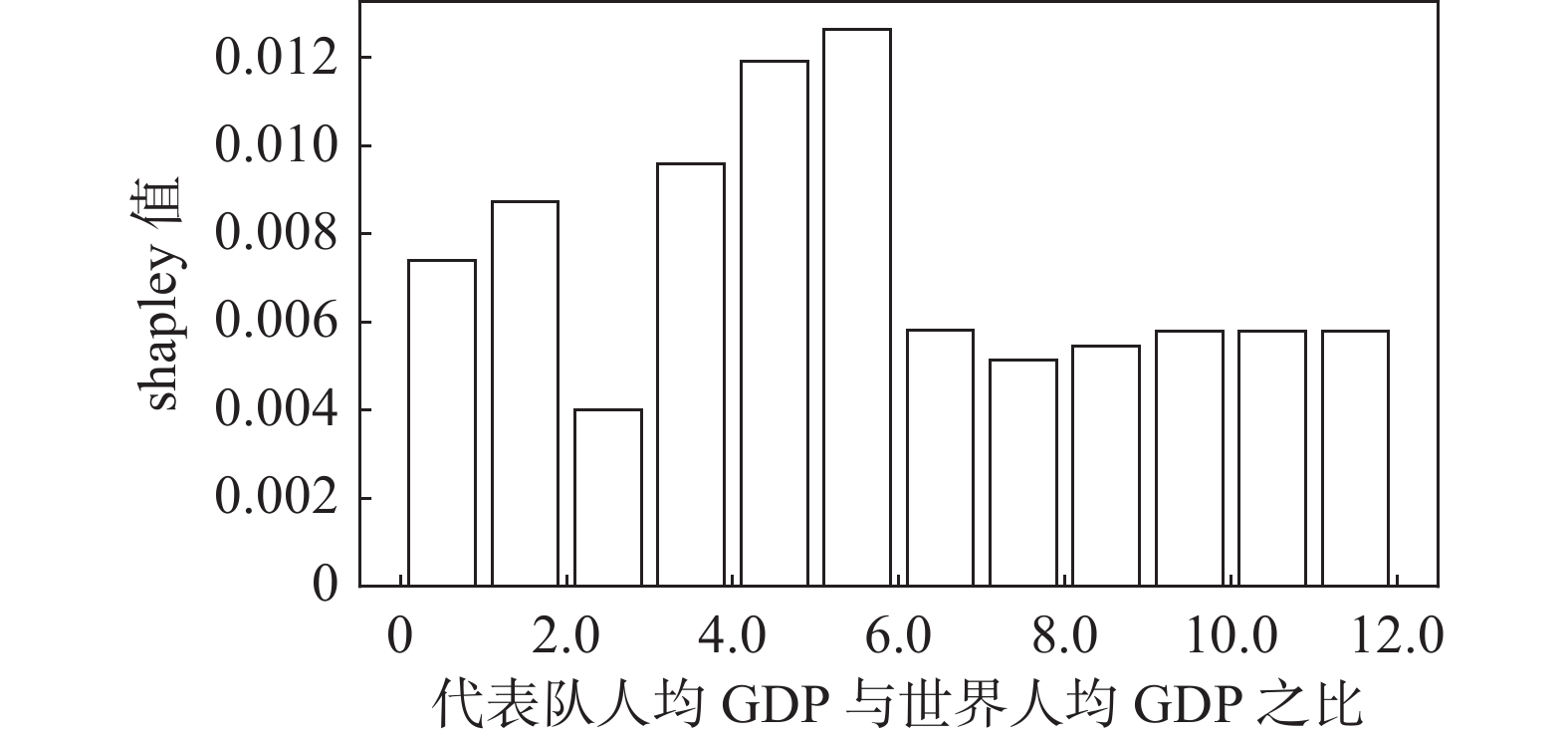
(3)除了上述项目出现了明显的根据人均收入的代表队项目匹配差异之外,还发现对于一些项目(如跳水)而言,各种人均收入水平的代表队都有所参与并且有可能获得奖牌,即GDP因素的各阶段在该项目上均能够有所收益。如图4所示,从人均GDP与世界人均GDP的比值小于1的代表队到人均GDP是世界人均GDP数倍的代表队,在各类样本点上,GDP因素对最终预测均有贡献。
3.6 预测2020年东京奥运会奖牌榜和实际奖牌榜的对比
在预测结果部分,基于分项目拟合模型对2020年东京奥运会的预测结果进行加总并与实际结果进行对比。在Schlembach等[2]的研究中,作者展示的预测结果能够很好地符合现实结果。但本文结果显示,在分项目对结果进行预测后,并没有提高对总体奖牌榜与金牌榜的预测能力(表9)。这主要是因为对数据按项目进行分组后,会显著降低每个项目中可用来训练的数据集。同时,模型预测结果和奥运会实际奖牌数之间存在一定差距,也说明体育赛事存在高度的不确定性,而这种不确定性也是竞技体育的魅力之一。
表 9 预测结果与实际结果对比Table 9. Comparison of predicted and actual outcomes/枚 代表队 奖牌数预测 实际奖
牌数代表队 金牌数预测 实际金
牌数不分性
别预测分性别
预测不分性
别预测分性别
预测美国 102 95 113 美国 36 36 39 中国 65 63 88 中国 22 19 38 俄罗斯 46 44 70 日本 8 7 27 英国 41 39 64 英国 14 14 21 日本 32 28 57 俄罗斯 16 10 20 澳大利亚 30 27 46 澳大利亚 7 4 17 意大利 24 20 38 荷兰 4 3 10 德国 35 31 37 意大利 4 4 10 荷兰 15 13 36 德国 8 8 10 法国 32 30 33 法国 8 7 10 4. 结论与建议
本文发现:①虽然都是基于相同时间尺度数据训练的模型,奥运会各项目的可预测性具有显著差异。对奖牌总数而言,可预测性最高的前十名项目分别是乒乓球、羽毛球、游泳、跳水、马术、击剑、柔道、自行车、摔跤和帆船。②在总体上,一个代表队所在国家或地区的人口越多、人均GDP越高、是该届奥运会的主办国,其获得的奖牌越多。这与Bernard等[1]的发现一致。③在特定项目上,若某国或地区具有潜在传统优势,那么该国家或地区的哑变量对该项目奖牌的预测贡献较大。以Shapley值为标准,代表队的潜在传统优势或特征对预测结果的贡献超过40%的项目有射箭、田径、拳击、击剑、体操、射击、游泳、举重和摔跤。④对项目金牌而言,随机森林模型对女子项目的预测准确性普遍高于男子项目。⑤经济发展水平不同的代表队,在奥运项目的选择上也存在差异。例如,自行车、马术、现代五项的参与代表队基本为发达经济体,而举重的参与代表队基本为发展中经济体。
本文对国家奥运争光战略和全民健身战略实施的政策意义:①作为一个快速发展的国家,我国应根据经济发展水平调整竞技体育发展战略。②在重点项目上加大投入,促进我国竞技体育的可持续发展。不应只关注金牌、奖牌的数量,而应对那些全球关注度高、参与度高、商业价值高、竞争激烈的项目加大投入。根据经济发展水平,以前瞻性的眼光加大重点项目的人才培养。③我国各个地区发展水平存在较大的差异,应制定差异化竞争的体育发展战略。如在东部沿海地区已有部分城市人均GDP接近发达经济体的水平,在这些区域应优先发展对经济水平依赖度较高的项目。④本文量化了我国各项目代表队的传统优势,该结果有助于制定竞技体育规划,例如选择垄断程度较低的项目作为我国体育发展的突破口。⑤全民健身是奥运争光的基础,我国是人口大国,全民参与为竞技体育的人才选拔提供了人口基数。我国应加大对重点项目全民参与的宣传和投入,如在足球、篮球等项目上加大对青少年的投入。
最后,本文的研究方法不仅限于分析体育项目,相同的研究方法也可用在其他领域(如科技、数学)的人才培养和竞争研究上。
作者贡献声明:石慧敏:提出论文选题,搜集统计数据,撰写论文;作者贡献声明:章东迎:调研文献,撰写、修改论文;作者贡献声明:章永辉:修改、指导修改论文。 -
表 1 预测所用的特征变量
Table 1 Characteristic variables for prediction
名称 定义 类型 GDPPC 人均GDP与世界人均GDP之比 连续变量 POP 人口占世界总人口的比重 连续变量 HOST 是否为举办国 0/1变量 LAST_HOST 是否为上一届举办国 0/1变量 NEXT_HOST 是否为下一届举办国 0/1变量 SOVIET 是否为社会主义政体 0/1变量 PLANNED 是否为计划经济体制 0/1变量 LAST_TOP8 上一届进入前八名的数量 连续变量 LAST_TOP3 上一届进入前三名的数量 连续变量 ISO 国家或地区哑变量 0/1变量 表 2 2020年东京奥运会奖/金牌数预测得分前十和后十的项目
Table 2 Top 10 and Bottom 10 predictable events in Tokyo Olympic awards/gold medal forecast
预测得分前十 预测得分后十 奖牌项目 得分 金牌项目 得分 奖牌项目 得分 金牌项目 得分 乒乓球 0.8453 花样游泳 0.9707 水球 −0.0226 跆拳道 −0.5780 羽毛球 0.8424 跳水 0.9082 现代五项 0.0582 网球 −0.3175 游泳 0.8339 乒乓球 0.8197 排球 0.1018 足球 −0.2599 跳水 0.8314 射箭 0.7868 网球 0.1664 现代五项 −0.1613 马术 0.7932 马术 0.6956 曲棍球 0.2307 排球 −0.1437 击剑 0.7139 摔跤 0.6809 举重 0.2494 皮划艇 −0.0767 柔道 0.7108 游泳 0.6540 铁人三项 0.2954 赛艇 0.1077 自行车 0.7058 篮球 0.6335 篮球 0.3001 铁人三项 0.1536 摔跤 0.6684 水球 0.6325 跆拳道 0.3921 射击 0.1892 帆船 0.6528 帆船 0.6253 射击 0.4967 手球 0.2301 表 3 对三大球项目影响前十的变量
Table 3 Top 10 important variables in three major ball events forecast
足球 篮球 排球 变量 Shapley值 变量 Shapley值 变量 Shapley值 POP 0.0491 LAST_TOP3 0.0463 LAST_TOP8 0.0586 GDPPC 0.0157 LAST_TOP8 0.0298 POP 0.0426 德国 0.0116 GDPPC 0.0163 LAST_TOP3 0.0410 LAST_TOP8 0.0101 美国 0.0155 GDPPC 0.0134 阿根廷 0.0085 POP 0.0154 巴西 0.0123 巴西 0.0083 澳大利亚 0.0086 意大利 0.0105 美国 0.0050 法国 0.0082 美国 0.0062 加拿大 0.0050 西班牙 0.0077 PLANNED 0.0043 LAST_TOP3 0.0043 塞尔维亚 0.0070 德国 0.0042 尼日利亚 0.0036 阿根廷 0.0051 HOST 0.0040 表 4 代表队固定效应对全样本奖牌预测值影响超过0.3的代表队和项目
Table 4 Teams and events with Shapley value greater than 0.3 for team fixed effect (full sample medals prediction)
项目 代表队 Shapley值 项目 代表队 Shapley值 射箭 韩国 0.4056 网球 捷克 0.3186 现代五项 俄罗斯 0.3083 俄罗斯 0.3019 帆船 英国 0.3557 田径 俄罗斯 0.4893 自行车 英国 0.3348 美国 0.4429 马术 德国 0.3035 白俄罗斯 0.3155 乒乓球 中国 0.3114 体操 俄罗斯 0.6031 跆拳道 韩国 0.3982 乌克兰 0.5039 柔道 乌兹别克斯坦 0.3624 白俄罗斯 0.3733 格鲁吉亚 0.3184 举重 哈萨克斯坦 0.4060 射击 俄罗斯 0.5194 格鲁吉亚 0.3601 斯洛伐克 0.3050 俄罗斯 0.3533 游泳 俄罗斯 0.5370 摔跤 俄罗斯 0.6216 美国 0.4977 白俄罗斯 0.3951 皮划艇 捷克 0.3718 哈萨克斯坦 0.3220 德国 0.3137 乌克兰 0.3173 跳水 中国 0.3324 拳击 俄罗斯 0.5723 俄罗斯 0.3051 哈萨克斯坦 0.5722 击剑 俄罗斯 0.5267 阿塞拜疆 0.3245 意大利 0.3147 乌克兰 0.3236 乌兹别克斯坦 0.3044 表 5 代表队固定效应对全样本金牌预测值影响超过0.3的代表队和项目
Table 5 Teams and events with Shapley value greater than 0.3 for team fixed effect (full sample gold medal prediction)
项目 代表队 Shapley值 项目 代表队 Shapley值 田径 俄罗斯 0.3454 花样游泳 俄罗斯 0.3820 击剑 俄罗斯 0.4430 游泳 俄罗斯 0.3663 摔跤 俄罗斯 0.5997 美国 0.3484 跳水 中国 0.5192 举重 中国 0.4188 帆船 巴西 0.3144 伊朗 0.4031 网球 美国 0.3698 体操 俄罗斯 0.3826 跆拳道 韩国 0.6042 乌克兰 0.3424 表 6 分性别奖牌数和金牌数预测得分前十的项目
Table 6 Top 10 predictable events for medals and gold medals (by gender)
奖牌项目 金牌项目 男子项目 得分 女子项目 得分 男子项目 得分 女子项目 得分 乒乓球 0.8601 曲棍球 0.7363 跳水 0.8926 跳水 0.9973 跳水 0.7914 跳水 0.6869 乒乓球 0.8909 花样游泳 0.9707 柔道 0.7011 田径 0.6729 帆船 0.7705 射箭 0.9693 摔跤 0.6957 足球 0.6664 水球 0.6054 水球 0.9339 赛艇 0.5854 游泳 0.6516 拳击 0.5598 乒乓球 0.9087 游泳 0.5748 体操 0.6439 摔跤 0.5494 篮球 0.8466 自行车 0.5739 花样游泳 0.6085 游泳 0.5196 自行车 0.5599 击剑 0.5350 手球 0.6062 柔道 0.4733 摔跤 0.5540 拳击 0.5273 乒乓球 0.5952 篮球 0.4298 柔道 0.5212 帆船 0.4885 皮划艇 0.5704 射箭 0.3715 游泳 0.4106 表 7 代表队固定效应对分性别项目奖牌预测值影响超过0.3的代表队和项目
Table 7 Teams and events with Shapley value greater than 0.3 for team fixed effect (medals prediction by gender)
性别 项目 代表队 Shapley值 性别 项目 代表队 Shapley值 男子 射箭 韩国 0.4141 女子 射箭 韩国 0.5035 田径 美国 0.5389 现代五项 英国 0.3027 帆船 英国 0.4546 游泳 美国 0.3843 乒乓球 中国 0.3503 皮划艇 匈牙利 0.3606 跆拳道 韩国 0.4352 跳水 中国 0.3328 自行车 英国 0.3418 击剑 意大利 0.3274 击剑 俄罗斯 0.4623 举重 泰国 0.3340 体操 俄罗斯 0.3672 田径 俄罗斯 0.5335 现代五项 俄罗斯 0.3249 肯尼亚 0.3431 射击 意大利 0.3668 摔跤 日本 0.3199 俄罗斯 0.3249 射击 俄罗斯 0.4702 游泳 俄罗斯 0.4860 乌克兰 0.3351 美国 0.4213 德国 0.3223 柔道 乌兹别克斯坦 0.3972 体操 俄罗斯 0.4419 日本 0.3441 美国 0.3639 格鲁吉亚 0.3297 乌克兰 0.3339 皮划艇 捷克 0.3889 网球 捷克 0.3112 斯洛伐克 0.3245 俄罗斯 0.3070 举重 哈萨克斯坦 0.4568 俄罗斯 0.4080 格鲁吉亚 0.3291 伊朗 0.3220 拳击 哈萨克斯坦 0.5482 俄罗斯 0.5266 乌克兰 0.3746 乌兹别克斯坦 0.3282 阿塞拜疆 0.3244 摔跤 俄罗斯 0.6487 白俄罗斯 0.4472 乌克兰 0.3544 格鲁吉亚 0.3219 哈萨克斯坦 0.3013 表 8 代表队固定效应对分性别项目金牌预测值影响超过0.3的代表队和项目
Table 8 Teams and events with Shapley value greater than 0.3 for team fixed effect (gold medals prediction by gender)
性别 项目 代表队 Shapley值 性别 项目 代表队 Shapley值 男子 拳击 俄罗斯 0.3046 女子 射箭 韩国 0.3349 跳水 中国 0.3611 田径 俄罗斯 0.4171 跆拳道 韩国 0.3514 跳水 中国 0.3691 举重 伊朗 0.3816 游泳 美国 0.3555 游泳 美国 0.3013 花样游泳 俄罗斯 0.3820 乒乓球 中国 0.3402 跆拳道 韩国 0.4079 摔跤 俄罗斯 0.6951 举重 中国 0.3996 帆船 英国 0.3229 摔跤 日本 0.3182 澳大利亚 0.3184 击剑 俄罗斯 0.3410 意大利 0.3046 表 9 预测结果与实际结果对比
Table 9 Comparison of predicted and actual outcomes
/枚 代表队 奖牌数预测 实际奖
牌数代表队 金牌数预测 实际金
牌数不分性
别预测分性别
预测不分性
别预测分性别
预测美国 102 95 113 美国 36 36 39 中国 65 63 88 中国 22 19 38 俄罗斯 46 44 70 日本 8 7 27 英国 41 39 64 英国 14 14 21 日本 32 28 57 俄罗斯 16 10 20 澳大利亚 30 27 46 澳大利亚 7 4 17 意大利 24 20 38 荷兰 4 3 10 德国 35 31 37 意大利 4 4 10 荷兰 15 13 36 德国 8 8 10 法国 32 30 33 法国 8 7 10 -
[1] BERNARD A B,BUSSE M R. Who wins the Olympic Games:Economic resources and medal totals[J]. Review of Economics and Statistics,2004,86(1):413-417 doi: 10.1162/003465304774201824
[2] SCHLEMBACH C,SCHMIDT S L,SCHREYER D,et al. Forecasting the Olympic medal distribution:A socioeconomic machine learning model[J]. Technological Forecasting and Social Change,2022,175:121314 doi: 10.1016/j.techfore.2021.121314
[3] LUNDBERG S M, ERION G G, LEE S I. Consistent individualized feature attribution for tree ensembles[EB/OL]. [2022-08-30]. http://arxiv.org/abs/1802.03888.pdf
[4] LUNDBERG S M, LEE S I. A unified approach to interpreting model predictions[C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. December 4-9, 2017, Long Beach, California, USA. ACM, 2017: 4768–4777
[5] 叶春明,赵圣文,杨秀红,等. 基于机器学习的青少年运动员新冠肺炎疫情应对能力分析与预测[J]. 体育学刊,2020,27(3):68-73 [6] 黄元琦,李玉榕,归予恒. 机器学习:运动损伤预防的新途径[J]. 福建体育科技,2021,40(1):12-18 doi: 10.3969/j.issn.1004-8790.2021.01.003 [7] 高素霞. 混沌理论和机器学习算法的运动员成绩预测模型[J]. 现代电子技术,2018,41(7):152-155 [8] ZHU P, SUN F. Sports athletes' performance prediction model based on machine learning algorithm[C]//ABAWAJY J, CHOO KK, ISLAM R, et al. International Conference on Applications and Techniques in Cyber Security and Intelligence. Cham: Springer, 2020: 498-505
[9] OYTUN M,TINAZCI C,SEKEROGLU B,et al. Performance prediction and evaluation in female handball players using machine learning models[J]. IEEE Access,2020,8:116321-116335 doi: 10.1109/ACCESS.2020.3004182
[10] HOOG ANTINK C,BRACZYNSKI A K,GANSE B. Learning from machine learning:Prediction of age-related athletic performance decline trajectories[J]. GeroScience,2021,43(5):2547-2559 doi: 10.1007/s11357-021-00411-4
[11] NAGLAH A, KHALIFA F, MAHMOUD A, et al. Athlete-customized injury prediction using training load statistical records and machine learning[C]//2018 IEEE International Symposium on Signal Processing and Information Technology (ISSPIT). Louisville, KY, USA. IEEE, 2018: 459-464
[12] BREIMAN L. Random forests[J]. Machine Learning,2001,45:5-32 doi: 10.1023/A:1010933404324
[13] ATHEY S,TIBSHIRANI J,WAGER S. Generalized random forests[J]. The Annals of Statistics,2019,47(2):1148-1178
[14] WAGER S,ATHEY S. Estimation and inference of heterogeneous treatment effects using random forests[J]. Journal of the American Statistical Association,2018,113(523):1228-1242 doi: 10.1080/01621459.2017.1319839
[15] 李斌,邵新月,李玥阳. 机器学习驱动的基本面量化投资研究[J]. 中国工业经济,2019(8):61-79 [16] 陈小亮,刘玲君,肖争艳,等. 生产部门通缩与全局性通缩影响因素的差异性研究:机器学习方法的新视角[J]. 中国工业经济,2021(7):26-44 doi: 10.3969/j.issn.1006-480X.2021.07.006 [17] MOLNAR C, GRUBER S, KOPPER P. Limitations of interpretable machine learning methods[EB/OL]. [2022-08-30]. https://slds-lmu.github.io/iml_methods_limitations





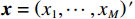
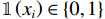
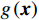
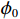
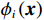
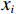
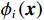
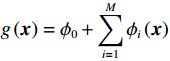
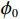
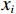
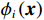
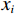
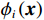
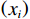
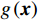
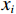
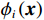
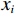
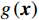
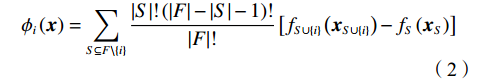
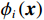
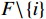
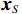
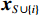
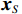
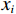
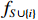
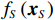
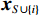
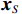
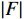
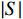
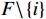
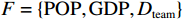
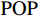
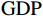

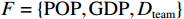
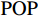
 下载:
下载: